Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

                                              (6)

Отсюда видно, что движение апериодическое и не имеет колебательного характера. Аналогичный характер будет иметь движение и в случае , когда общее решение имеет вид

                                                      (7)

Легко заметить,  что  в обоих  последних  случаях при  имеем .

Если заданы начальные условия  и , то в случае, когда , имеем , а . Решая эту систему относительно  и , получим

,       

и, следовательно

 

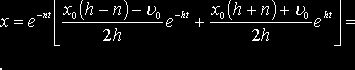
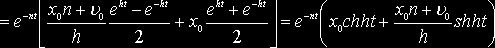
В случае же, когда , получаем ,  и следовательно,

Вынужденные колебания без учета сопротивления среды.

Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.

Пусть груз весом Р подвешен на вертикальной пружине, длина которой в ненагруженном состоянии равна . На груз действует периодическая возмущающая сила  где Q и р — постоянные. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.

Решение

Как и для гармонических колебаний, получаем уравнение

Полагая, как и прежде,  и, кроме того,  перепишем уравнение в виде

                                               (8)

Это—неоднородное линейное уравнение второго порядка с постоянными коэффициентами, причем однородным уравнением, соответствующим уравнению (8), является (1). Поэтому ; остается найти х. Если предположить, что , то частное решение х, нужно искать в виде , где М и N — коэффициенты, подлежащие определению. Итак,

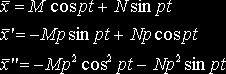
Производя вычисления, получаем

     

откуда М=0 и  Полученное таким образом частное решение

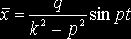                                                     (9)

определяет так называемые вынужденные колебания, созданные возмущаю-щей силой . Вынужденные колебания, имеют тот же период, что и возмущающая сила, совпадают с ней по фазе (т. е. имеют одинаковую начальную фазу) при k>p, либо отличаются на p, если k<p, т. е. если N<0.

Рекомендуем скачать другие рефераты по теме: сочинение, реферат расчеты.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки