Из таблицы 1 находим 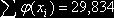 . Искомая оценка
. Искомая оценка
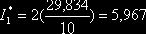
§3. Способ существенной выборки, использующий
«вспомогательную плотность распределения».
В качестве оценки интеграла 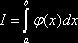 принимают
принимают 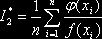 , где n – число испытаний; f(x) – плотность распределения
«вспомогательной» случайной величины X, причём
, где n – число испытаний; f(x) – плотность распределения
«вспомогательной» случайной величины X, причём 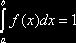 ;
; 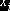 - возможные значения
X, которые разыгрывают по формуле
- возможные значения
X, которые разыгрывают по формуле 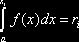 .
.
Функцию f(x) желательно выбирать так, чтобы отношение 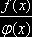 при различных
значениях x изменялось незначительно. В частности, если
при различных
значениях x изменялось незначительно. В частности, если 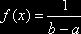 , то получим оценку
, то получим оценку  .
.
Задача. Найти оценку 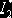 интеграла
интеграла 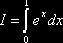 .
.
Решение. Так как  , то в качестве плотности распределения «вспомогательной»
случайной величины X примем функцию
, то в качестве плотности распределения «вспомогательной»
случайной величины X примем функцию 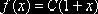 . Из условия
. Из условия 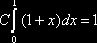 найдём
найдём 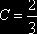 . Итак,
. Итак, 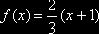 .
.
Запишем искомый интеграл так:
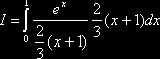 .
.
Таким образом, интеграл I представлен в виде математического
ожидания функции 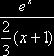 . В качестве искомой оценки примем выборочную среднюю (для
простоты ограничимся десятью испытаниями):
. В качестве искомой оценки примем выборочную среднюю (для
простоты ограничимся десятью испытаниями):
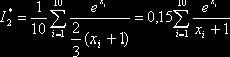 ,
,
где 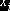 - возможные значения
X, которые надо разыграть по известной плотности
- возможные значения
X, которые надо разыграть по известной плотности 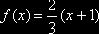 . По правилу (для того, чтобы разыграть возможное значение
. По правилу (для того, чтобы разыграть возможное значение  непрерывной случайной
величины X, зная её плотность вероятности f(x), надо выбрать случайное число
непрерывной случайной
величины X, зная её плотность вероятности f(x), надо выбрать случайное число  и решить относительно
и решить относительно  уравнение
уравнение
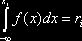 , или уравнение
, или уравнение 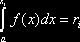 ,
,
где a – наименьшее конечно возможное значение X), имеем 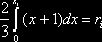 . Отсюда находим явную формулу для разыгрывания возможных
значений X:
. Отсюда находим явную формулу для разыгрывания возможных
значений X:
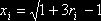 .
.
В таблице 2 приведены результаты 10 испытаний.
Сложив числа последней строки таблицы 2, получим 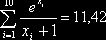 . Искомая оценка равна
. Искомая оценка равна 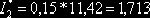 .
.
Таблица 2.

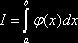 принимают
принимают 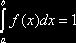 ;
; 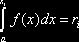 .
.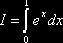 .
.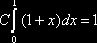 найдём
найдём 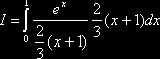 .
.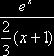 . В качестве искомой оценки примем выборочную среднюю (для
простоты ограничимся десятью испытаниями):
. В качестве искомой оценки примем выборочную среднюю (для
простоты ограничимся десятью испытаниями): 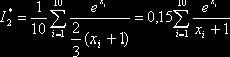 ,
, 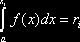 ,
, 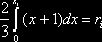 . Отсюда находим явную формулу для разыгрывания возможных
значений X:
. Отсюда находим явную формулу для разыгрывания возможных
значений X: