|
1,009
1,345
1,044
1,084
1,139
1,015
1,291
1,118
1,077
1,298
|
§4. Способ, основанный на истолковании интеграла как
площади.
Пусть подынтегральная функция неотрицательна и
ограничена: 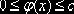 , а двумерная случайная величина
, а двумерная случайная величина 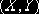 распределена
равномерно в прямоугольнике D с основанием
распределена
равномерно в прямоугольнике D с основанием  и высотой
и высотой  . Тогда двумерная плотность вероятности
. Тогда двумерная плотность вероятности 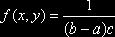 для точек, принадлежащих D;
для точек, принадлежащих D; 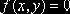 вне D.
вне D.
В качестве оценки интеграла 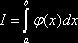 принимают
принимают 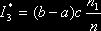 , где n – общее число случайных точек
, где n – общее число случайных точек 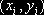 , принадлежащих D;
, принадлежащих D; 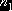 - число случайных
точек, которые расположены под кривой
- число случайных
точек, которые расположены под кривой 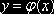 .
.
Задача. Найти оценку 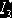 интеграла
интеграла 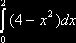 .
.
Решение. Используем формулу 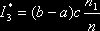 .
.
В интервале (0,2) подынтегральная функция 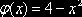 неотрицательна и
ограничена, причём
неотрицательна и
ограничена, причём 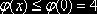 ; следовательно, можно принять c=4.
; следовательно, можно принять c=4.
Введём в рассмотрение двумерную случайную величину
(X,Y), распределённую равномерно в прямоугольнике D с основанием 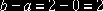 и высотой с=4, плотность вероятности которой
и высотой с=4, плотность вероятности которой 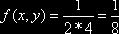 .
.
Разыгрываем n=10 случайных точек 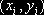 , принадлежащих прямоугольнику D. Учитывая, что составляющая
X в интервале (0,2) распределена равномерно с плотностью
, принадлежащих прямоугольнику D. Учитывая, что составляющая
X в интервале (0,2) распределена равномерно с плотностью 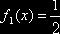 и составляющая Y в интервале
(0,4) распределена равномерно с плотностью
и составляющая Y в интервале
(0,4) распределена равномерно с плотностью 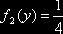 , разыграем координаты случайной точки
, разыграем координаты случайной точки 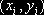 , принадлежащей прямоугольнику D, по паре независимых
случайных чисел
, принадлежащей прямоугольнику D, по паре независимых
случайных чисел 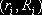 :
: 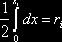 ,
, 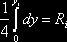 .Отсюда
.Отсюда 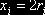 ,
, 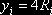 .
.

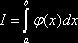 принимают
принимают 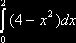 .
.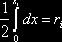 ,
, 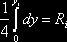 .Отсюда
.Отсюда