Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Если для полиномов f(x) и g(x) из K[x] существует такой полином , что f(x) = g(x)h(x), то говорят, что полином f(x) делится на полином g(x). Наша ближайшая задача заключается в выяснении вопроса о делимости  на линейный двучлен x - c при .

Прежде всего установим, что всегда осуществимо так называемое деление с остатком:  при . Здесь полином h(x) называется неполным частным, а r - остатком.

Теорема 2. Пусть  и . Найдутся полином  и элемент  такие, что . При этом .

Доказательство.  Естественно искать h(x) в форме . Сравнение коэффициентов многочлена в левой части равенства  = = с коэффициентами многочлена, полученного после раскрытия скобок и приведения подобных, в правой части этого равенства приводит к цепочке равенств

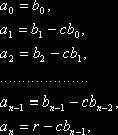
откуда последовательно определяют коэффициенты h(x) и остаток r:

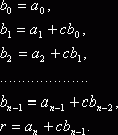                                                (8)

Равенство  непосредственно следует из равенства  после подстановки в последнее вместо x элемент c.

Теорема доказана. Кроме того, получен очень удобный способ вычисления коэффициентов h(x) и остатка r. Этот способ носит название схемы Горнера. Вычисления удобно располагать в виде таблицы:

	a0	a1	a2	...	an-1	an
c	b0	b1	b2	...	bn-1	c

Элементы нижней строки вычисляются последовательно по формулам (8): b0 = a0, a каждый последующий элемент равен сумме элемента, находящегося над ним, и предыдущего элемента нижней строки, умноженного на x0.

Элемент c кольца K называется корнем полинома f(x), если .

Следствие (теорема Безу). Многочлен f(x) делится на  в кольце K[x]  тогда и только тогда, когда c - его корень.

Рекомендуем скачать другие рефераты по теме: план конспект, реферат по праву.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки