Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

где n-число наблюдений;

m – число факторов.

Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:

Частный F-критерий оценивает статистическую значимость присутствия каждого факторов в уравнении. В общем виде для фактора  частный F-критерий определится как

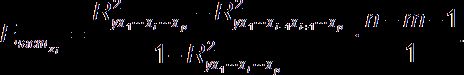
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения

где  - средняя квадратичная ошибка коэффициента регрессии  она может быть определена по следующей формуле:

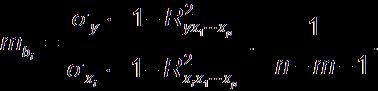
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности.

Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы   были бы равны нулю. Так, для включающего три объясняющих переменных уравнения

матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:

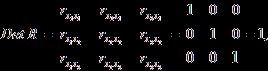
так как  и .

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

.

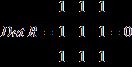Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных . Доказано, что величина  имеет приближенное распределение  с степенями свободы. Если фактическое значение  превосходит табличное (критическое) , то гипотеза  отклоняется. Это означает, что , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора  остатки  имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.

При нарушении гомоскедастичности мы имеем неравенства

Рекомендуем скачать другие рефераты по теме: реферат менеджмент, сочинение описание.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки