
Некоторые вопросы геометрии вырожденных треугольников
Категория реферата: Рефераты по математике
Теги реферата: курсовые работы, рефераты
Добавил(а) на сайт: Чаадаев.
1 2 3 4 | Следующая страница реферата
Некоторые вопросы геометрии вырожденных треугольников.
Казакова Г.Г. , доцент кафедры геометрии ХГПУ
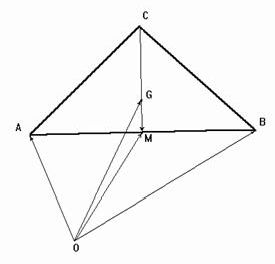
Рисунок 1. Центроид треугольника
Применение методов векторной алгебры позволяет выявлять те особые свойства фигур, которые могут ускользнуть от нас при их наглядно-геометрическом рассмотрении, и при этом не потерять геометрическую наглядность изучаемого факта (как это часто бывает при применении метода координат).
Остановимся на некоторых фактах, связанных с геометрией треугольника, которые позднее будут применены к вырожденным треугольникам, что позволит получить интересные результаты.
Договоримся об обозначениях: точки будем обозначать заглавными буками обычным шрифтом (например: А, B) , а радиус-векторы точек (и обычные векторы) - жирным курсивом (например A, G, BC, b).
1. Центроид треугольника. Точка G пересечения медиан треугольника АВС называется его центроидом. Выразим радиус-вектор G центроида через радиус-векторы A, B, C вершин треугольника при любом выборе начала векторов - точки О.
По свойству медиан треугольника CG:GM=2 (смотри рис.1), следовательно G=(C+2M)/3, где М - середина стороны АВ, т.е. M=(A+B)/2. Итак,
G=(A+B+C)/3 (1)
Верно и обратное: если точки А, В и С не коллинеарны и имеет место условие (1), то точка G есть центроид треугольника АВС. В самом деле, пусть точка М - середина отрезка АВ, т. е. при любом выборе начала векторов О имеем M=(A+B)/2. Тогда из равенства (1) получим G=(C+2M)/3, т.е. G делит медиану СМ в отношении 2:1 и потому является центроидом треугольника АВС.
2. Ортоцентр треугольника. Прямая Эйлера. Если за начало векторов взять центр О описанной вокруг треугольника АВС окружности, то радиус-вектор ортоцентра Н (точки пересечения высот) этого треугольника равен
H = A+B+C (2)
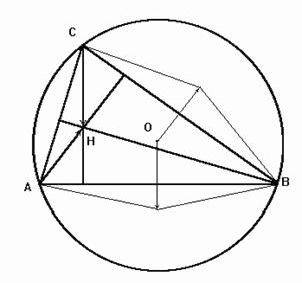
Рисунок 2. Ортоцентр треугольника
В самом деле, векторы A+B и H-C (смотри рис.2) коллинеарны, значит, A+B = l(H-C).
По этой же причине B+C = m(H-A).
После почленного вычитания этих равенств получаем:
A-C = (l - m)H - lC + mA или
(1 - m)A + (l - 1)C + (m - l)H = 0
и при этом сумма коэффициентов
(1 - m) + (l - 1) + (m - l) = 0.
Выполнение двух этих условий возможно только в двух случаях:
либо когда точки А, С и Н коллинеарны (это невозможно по условию), либо когда
(1 - m) = (l - 1) = (m - l) = 0.
Рекомендуем скачать другие рефераты по теме: курсовые работы, уголовное право шпаргалки.
1 2 3 4 | Следующая страница реферата