Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Если вершины В и С треугольника АВС совпали, то сторона ВС = а будет касательной к описанной около треугольника окружности в этой точке, а длина стороны ВС будет равна нулю.

Итак, определить треугольник с двумя совпавшими вершинами (вырожденный треугольник) можно двояко:

1) это хорда АВ окружности с одним двойным концом В;

2) это отрезок АВ и прямая, проходящая через его точку В.

В последнем случае описанная около треугольника АВС окружность касается прямой а в точке В, лежащей на ней. Такая окружность - единственная.

В полученном треугольнике с двумя совпавшими вершинами величина угла А равна нулю, а углы В и С - смежные, поэтому сумма внутренних углов треугольника равна 1800. Рассмотрим интерпретацию для данного треугольника свойств невырожденного треугольника.

Так, при любом выборе начала О векторов G=1/3(A+2B), т.е. центроид G делит отрезок АВ в отношении л=2:1. Ортоцентр Н определится как тоже пересечение высоты АHi ^ а и двойной высоты, проходящей через точку В є С перпендикулярно к АВ. Если за начало векторов принять центр О описанной окружности, то Н = А + 2В (рис.5).

Итак, векторы G и Н коллинеарны и OG : GH = 1 : 2.

Применительно к данному случаю теорема 1 звучит следующим образом:

Если АВ - хорда окружности, а - касательная к ней в точке В и перпендикуляры из точки А к прямой а из точки В у прямой АВ пересекаются в точке Н, то точки Е, F и K, симметричные Н соответственно относительно а, В и середины АВ, принадлежат данной окружности (рис.5).

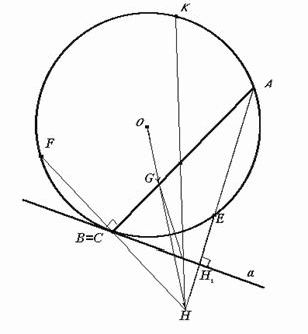Рисунок 5

Для обычного треугольника имеет место теорема Симпсона:

ортогональные проекции точки окружности на стороны вписанного в нее треугольника лежат на одной прямой, называемой прямой Симпсона для данного треугольника.

Для треугольника вырожденного этот факт тривиален: точки М1 и М2 совпали, а две точки М1 є М2 и М3 всегда определяют прямую линию (рис.6).

Однако, так как DММ1В~DММ3А, (они прямоугольные и углы МВМ1 и МАМ3 измеряются половиной дуги МnB), то МВ : МА = ММ2 : ММ3 или МВ · ММ3 = МА · ММ2, т.е. получаем теорему 3:

Если АВ - хорда окружности и а - касательная к ней в точке В, то произведение расстояний произвольной точки окружности до точки касания и до хорды равно произведению расстояний этой точки до второго конца хорды и до касательной.

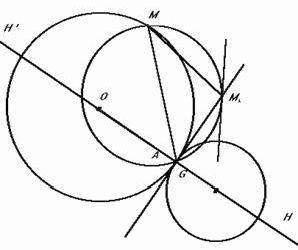
Рисунок 7

Теорема 2 (об окружности девяти точек треугольника) для вырожденного треугольника может быть сформулирована так:

Если АВ - хорда окружности, а - касательная к ней в точке В и перпендикуляры АH1 к прямой а и FB к прямой АВ пересекаются в точке Н (рис.5), то основания H1 и В этих перпендикуляров и середины отрезков АВ, АН и ВН лежат на одной окружности, радиус которой равен половине радиуса данной окружности.

Треугольник с тремя совпавшими вершинами (дважды вырожденный треугольник).

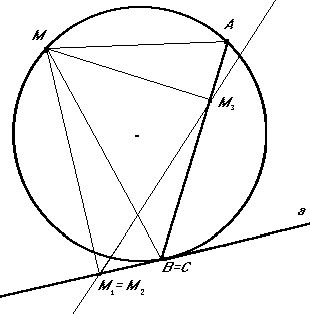
Рисунок 6

Такой треугольник можно задать с помощью точки А окружности (рис.7). В этом случае все три стороны совпадают, ибо А=В=С, и являются касательной а к окружности в точке А. Если за начало векторов принять центр О описанной окружности, то G=A и H=3A, т.е. ОАН - прямая Эйлера для вырожденного треугольника и OG:GH=1:2. Точка Н', симметричная Н относительно сторон и середин сторон вырожденного треугольника АВС, лежит на окружности (О,ОА), описанной около этого треугольника.

Чтобы выяснить положение прямой Симпсона, обратимся к рис.6. Так как РММ1В = РММ3В = 900 , то точки М1 є М2 и М3 принадлежат окружности диаметра МВ. Следовательно, если А=В, то прямая М1М3 Симпсона будет касательной в точке М1 к окружности диаметра МА=МВ (рис.7).

Рекомендуем скачать другие рефераты по теме: курсовые работы, уголовное право шпаргалки.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки