Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Значит, имеет место последнее:

m = l = 1

и тогда H = A+B+C.

Так как при любом выборе начала векторов точки О

G=(A+B+C)/3

то в данном случае G = H/3, т. е. точки О, G и Н коллинеарны и OG : GH = 1:2. Прямая OGH называется прямой Эйлера для треугольника АВС.

Теорема 1: Точки, симметричные ортоцентру треугольника относительно его сторон и середин сторон, лежат на окружности, описанной вокруг этого треугольника.

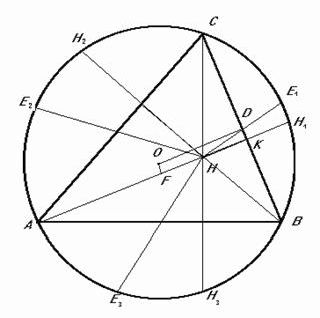
Рисунок 3.

Доказательство: Примем центр описанной окружности за начало радиус - векторов точек. Если точка Е1 симметрична Н относительно середины стороны ВС (смотри рис.3), то :

(B+C)/2 = (H+E1)/2, или

E1 = B + C - H = -A, т.е. точки A и E1 диаметрально противоположные и

E12 =A2 =R2.

Пусть прямая АН пересекает прямую ВС в точке К, а окружность - в точке Н1. Если ОД перпендикулярна ВС и ОF перпендикулярна АК, то:

K = D+F, D = (В+C)/2, F = (A+H1)/2 и, значит, K = (B+C+А+H1)/2 = (H+H1)/2 , т.е. Н1 симметрична точке Н относительно прямой ВС. Для точек Н2 и Н3 доказательство аналогично.

Теорема 2: Во всяком треугольнике середины сторон, основания высот и три точки, делящие пополам отрезки высот от вершин до ортоцентра, лежат на одной окружности, называемой окружностью девяти точек треугольника.

Доказательство: За начало векторов примем центр О описанной около треугольника окружности (смотри рис.4). Обозначим через Оi середины сторон, через Нi основания высот, через Кi середины отрезков высот от ортоцентра до вершины (i =1, 2 ,3).

Если L - середина отрезка ОН, то

L = H/2 = (A + B + C)/2,

LO1 = O1 - L = (B + C)/2 -(A+B+C)/2 = -A/2,

LK1 = K1 - L = (A + H)/2 - H/2 = A/2.

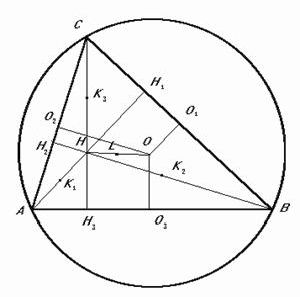
Рисунок 4.

Таким образом, точки Оi и Кi (i =1, 2 ,3) симметричны относительно L, т.е. принадлежат окружности с центром L и радиусом, равным половине радиуса R описанной окружности, так как LO12 = LK12 = (±A/2)2 = R2/4. Углы ОiHiKi ( i=1, 2, 3) прямые и опираются на диаметры полученной окружности, а поэтому точки Hi этой окружности принадлежат. В дальнейшем остановимся на применении рассмотренных фактов к вырожденным треугольникам, т.е. таким треугольникам, у которых совпадает две или три вершины.

3. Треугольник с двумя совпавшими вершинами.

Рекомендуем скачать другие рефераты по теме: курсовые работы, уголовное право шпаргалки.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки