
–Ě–Ķ–Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–į—Ź –ļ—Ä–į–Ķ–≤–į—Ź –∑–į–ī–į—á–į –ī–Ľ—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —Ā–ľ–Ķ—ą–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–ł–Ņ–į —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į —Ā –ļ—Ä–į—ā–Ĺ—č–ľ–ł —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į–ľ–ł
–ö–į—ā–Ķ–≥–ĺ—Ä–ł—Ź —Ä–Ķ—Ą–Ķ—Ä–į—ā–į: –†–Ķ—Ą–Ķ—Ä–į—ā—č –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ
–Ę–Ķ–≥–ł —Ä–Ķ—Ą–Ķ—Ä–į—ā–į: –Ī–Ķ—Ā–Ņ–Ľ–į—ā–Ĺ—č–Ķ –ī–ł–Ņ–Ľ–ĺ–ľ—č, —Ā–ļ–į—á–į—ā—Ć –ļ–ĺ–Ĺ—ā—Ä–ĺ–Ľ—Ć–Ĺ—É—é
–Ē–ĺ–Ī–į–≤–ł–Ľ(–į) –Ĺ–į —Ā–į–Ļ—ā: Bol'shakov.
–ü—Ä–Ķ–ī—č–ī—É—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į | 1 2 3 4 5 6 | –°–Ľ–Ķ–ī—É—é—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į
![]()
![]()  (26)
 (26)
–≥–ī–Ķ —Ā–ł–Ĺ–≥—É–Ľ—Ź—Ä–Ĺ—č–Ļ –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä S –∑–į–ī–į—Ď—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ¬†‚Äď –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł, –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č–Ķ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–į 0 £
t £
x £
1, 0 £
x £
t £
1, 0 £
x £
1, –Ņ—Ä–ł—á–Ķ–ľ
¬†‚Äď –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł, –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č–Ķ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–į 0 £
t £
x £
1, 0 £
x £
t £
1, 0 £
x £
1, –Ņ—Ä–ł—á–Ķ–ľ ![]() ,
, ![]() .
.
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī—Ź —Ä–Ķ–≥—É–Ľ—Ź—Ä–ł–∑–į—Ü–ł—é —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (26) –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –ö–į—Ä–Ľ–Ķ–ľ–į–Ĺ–į ‚Äď –í–Ķ–ļ—É–į [4] –ł –ī–Ķ–Ľ–į—Ź –Ĺ–Ķ—Ā–Ľ–ĺ–∂–Ĺ—č–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź, –ĺ–Ĺ–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā—Ā—Ź –ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é –§—Ä–Ķ–ī–≥–ĺ–Ľ—Ć–ľ–į —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ —Ä–ĺ–ī–į [2]:
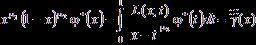 , (27)
, (27)
–≥–ī–Ķ
![]() ¬†–Ņ—Ä–ł—á–Ķ–ľ —Ź–ī—Ä–ĺ
¬†–Ņ—Ä–ł—á–Ķ–ľ —Ź–ī—Ä–ĺ ![]() ¬†–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź
¬†–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź ![]() ¬†–ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł, 0£
x, t£
1, 0£
x£
1.
¬†–ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł, 0£
x, t£
1, 0£
x£
1.
–°–Ľ–Ķ–ī—É—Ź
[2], –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ —á–Ķ—Ä–Ķ–∑ ![]() ¬†‚Äď –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —Ą—É–Ĺ–ļ—Ü–ł–Ļ
¬†‚Äď –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —Ą—É–Ĺ–ļ—Ü–ł–Ļ ![]() , –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö
–≤—Ā—é–ī—É –ļ—Ä–ĺ–ľ–Ķ –Ī—č—ā—Ć –ľ–ĺ–∂–Ķ—ā —ā–ĺ—á–Ķ–ļ x=0, (x=1) –ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł—Ö —É—Ā–Ľ–ĺ–≤–ł—é
, –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö
–≤—Ā—é–ī—É –ļ—Ä–ĺ–ľ–Ķ –Ī—č—ā—Ć –ľ–ĺ–∂–Ķ—ā —ā–ĺ—á–Ķ–ļ x=0, (x=1) –ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł—Ö —É—Ā–Ľ–ĺ–≤–ł—é ![]() ¬†
¬†![]() ¬†–≥–ī–Ķ
¬†–≥–ī–Ķ ![]() ,
, ![]() ‚Äď —Ü–Ķ–Ľ–į—Ź —á–į—Ā—ā—Ć
‚Äď —Ü–Ķ–Ľ–į—Ź —á–į—Ā—ā—Ć ![]() ,
, ![]() ‚Äď —Ü–Ķ–Ľ–į—Ź —á–į—Ā—ā—Ć
‚Äď —Ü–Ķ–Ľ–į—Ź —á–į—Ā—ā—Ć ![]() ¬†[1].
 [1].
–í
—Ä–į–Ī–ĺ—ā–Ķ [2] –Ĺ–į–Ļ–ī–Ķ–Ĺ—č –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ—č–Ķ –ł –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ—č–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź
—É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (27) –≤ –ļ–Ľ–į—Ā—Ā–Ķ ![]() .
.
–§—É–Ĺ–ļ—Ü–ł—Ź
![]() , –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–į—Ź
—Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ (21), –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā –ļ–Ľ–į—Ā—Ā—É –ł—Ā–ļ–ĺ–ľ—č—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (8).
, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–į—Ź
—Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ (21), –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā –ļ–Ľ–į—Ā—Ā—É –ł—Ā–ļ–ĺ–ľ—č—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (8).
–ü–ĺ—Ā–Ľ–Ķ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź ![]() , —Ą—É–Ĺ–ļ—Ü–ł—Ź
, —Ą—É–Ĺ–ļ—Ü–ł—Ź ![]() ¬†–∑–į–ī–į—Ď—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ (12). –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤
–ĺ–Ī–Ľ–į—Ā—ā–ł
¬†–∑–į–ī–į—Ď—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ (12). –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤
–ĺ–Ī–Ľ–į—Ā—ā–ł ![]() ¬†–Ņ—Ä–ł—Ö–ĺ–ī–ł–ľ –ļ –∑–į–ī–į—á–Ķ [6]: –Ĺ–į–Ļ—ā–ł —Ä–Ķ–≥—É–Ľ—Ź—Ä–Ĺ–ĺ–Ķ –≤
–ĺ–Ī–Ľ–į—Ā—ā–ł
¬†–Ņ—Ä–ł—Ö–ĺ–ī–ł–ľ –ļ –∑–į–ī–į—á–Ķ [6]: –Ĺ–į–Ļ—ā–ł —Ä–Ķ–≥—É–Ľ—Ź—Ä–Ĺ–ĺ–Ķ –≤
–ĺ–Ī–Ľ–į—Ā—ā–ł ![]() ¬†—Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (1), –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –≤–ľ–Ķ—Ā—ā–Ķ —Ā
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ
¬†—Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (1), –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –≤–ľ–Ķ—Ā—ā–Ķ —Ā
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ ![]() ¬†–≤ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł
¬†–≤ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł ![]() ¬†–ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–Ķ–Ķ –≥—Ä–į–Ĺ–ł—á–Ĺ—č–ľ —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ (4) –ł
¬†–ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–Ķ–Ķ –≥—Ä–į–Ĺ–ł—á–Ĺ—č–ľ —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ (4) –ł ![]() .
.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ–Ļ –∑–į–ī–į—á–ł –∑–į–ī–į–Ķ—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ :
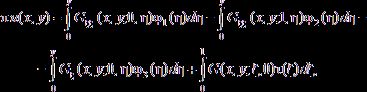
–≥–ī–Ķ
![]() ¬†‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź –ď—Ä–ł–Ĺ–į —ć—ā–ĺ–Ļ –∑–į–ī–į—á–ł –ī–Ľ—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
¬†‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź –ď—Ä–ł–Ĺ–į —ć—ā–ĺ–Ļ –∑–į–ī–į—á–ł –ī–Ľ—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
![]() . (28)
. (28)
–§—É–Ĺ–ļ—Ü–ł—Ź –ď—Ä–ł–Ĺ–į –≤—č—Ä–į–∂–į–Ķ—ā—Ā—Ź —á–Ķ—Ä–Ķ–∑ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (28), –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–ľ–Ķ—é—ā –≤–ł–ī:
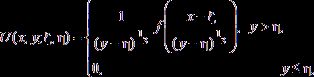
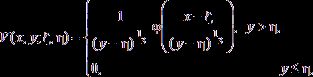
–≥–ī–Ķ
![]() ;
;
![]() ;
;
![]() ‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź
–Ď–Ķ—Ā—Ā–Ķ–Ľ—Ź. –§—É–Ĺ–ļ—Ü–ł–ł
‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź
–Ď–Ķ—Ā—Ā–Ķ–Ľ—Ź. –§—É–Ĺ–ļ—Ü–ł–ł ![]() ,
, ![]() ¬†–Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł –≠–Ļ—Ä–ł –ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—ā
—É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é
¬†–Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł –≠–Ļ—Ä–ł –ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—ā
—É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é ![]() . –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ
—Ā–≤–ĺ–Ļ—Ā—ā–≤–į —Ą—É–Ĺ–ļ—Ü–ł–Ļ
. –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ
—Ā–≤–ĺ–Ļ—Ā—ā–≤–į —Ą—É–Ĺ–ļ—Ü–ł–Ļ ![]() ¬†–ł
¬†–ł ![]() , –ł—Ö –ĺ—Ü–Ķ–Ĺ–ļ–ł
–≤–ľ–Ķ—Ā—ā–Ķ —Ā —á–į—Ā—ā–Ĺ—č–ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į –Ī–ĺ–Ľ—Ć—ą–Ķ 1, –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ—č –≤ [7].
, –ł—Ö –ĺ—Ü–Ķ–Ĺ–ļ–ł
–≤–ľ–Ķ—Ā—ā–Ķ —Ā —á–į—Ā—ā–Ĺ—č–ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į –Ī–ĺ–Ľ—Ć—ą–Ķ 1, –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ—č –≤ [7].
–°–Ņ–ł—Ā–ĺ–ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä—č
–Ď–ł—Ü–į–ī–∑–Ķ –ź.–í. –Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ļ–Ľ–į—Ā—Ā—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –≤ —á–į—Ā—ā–Ĺ—č—Ö –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö. –ú.: –Ě–į—É–ļ–į, 1981.
–†–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī—É–Ķ–ľ —Ā–ļ–į—á–į—ā—Ć –ī—Ä—É–≥–ł–Ķ —Ä–Ķ—Ą–Ķ—Ä–į—ā—č –Ņ–ĺ —ā–Ķ–ľ–Ķ: –Ņ–ĺ–Ľ–ł—ā–ĺ–Ľ–ĺ–≥–ł—Ź —ą–Ņ–į—Ä–≥–į–Ľ–ļ–ł, —Ä–Ķ—Ą–Ķ—Ä–į—ā –ľ–Ķ—ā–į–Ľ–Ľ—č.
–ü—Ä–Ķ–ī—č–ī—É—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į | 1 2 3 4 5 6 | –°–Ľ–Ķ–ī—É—é—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į