Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Если N = 1001, тогда возникает проблема: какая линия сфотографировалась дважды?

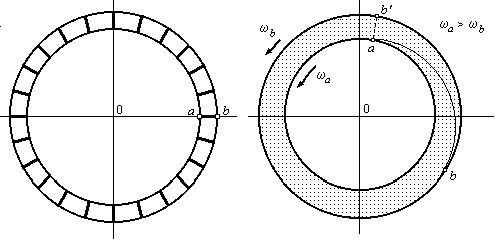
Рис. 1. Парадоксы вращающегося кольца

Рассмотрим другой вариант парадокса с этим кольцом. Согласно Специальной теории относительности внешний (периферийный) край кольца должен иметь меньшую угловую скорость, чем внутренний (см. рис.1, правое кольцо). По этой причине точка «a» кольца будет «убегать» относительно точки «b». Линия ab окажется уже не радиальной (как в классической механике ab'), а будет с течением времени удлиняться, напоминая кольцевую спираль, число витков которой постоянно растет. Если мы быстро остановим кольцо, как будет вести себя эта спираль? Сразу станет «радиальным отрезком» или же будет некоторое время «раскручиваться»? Будет ли наблюдатель, вращающийся вместе с кольцом, наблюдать этот эффект?

Парадоксы вращательного движения имеют давнюю историю. Процитируем историю «парадокса Эренфеста» [3]:

«Суть (преобразования Лоренца – прим. наше) сводится к следующему: продольные – в направлении движения – размеры быстро движущегося тела сокращаются. Еще в 1909 году известный физик Пауль Эренфест усомнился в этом выводе. Вот его возражение: допустим, движущиеся предметы, действительно сокращаются. Хорошо, проведем опыт с диском. Будем вращать его, постепенно увеличивая скорость. Размеры диска, как говорит г-н Эйнштейн, будут уменьшаться; кроме того, диск искривится. Когда же скорость диска достигнет скорости света, диск попросту исчезнет. Эйнштейн оказался в шоке, потому, что Эренфест был прав ... а затем (Эйнштейн – прим. наше) помог оппоненту получить должность профессора физики ... В свою очередь, со страниц книг о частной теории относительности исчезает ... парадокс Эренфеста»

Итак, в рамках СТО пространство в движущихся системах отсчета реально сжимается, а время столь же реально замедляется. Если это так, пространственно-временные искажения должны отразиться и на процессах взаимодействий для всех без исключения явлений природы. И здесь сразу же возникли, так называемые, динамические парадоксы.

Рассмотрим парадокс рычага. Представим себе Г-образный рычаг, изображенный на рис.2. Этот рычаг уравновешен силами. Если мы теперь будем двигаться относительно этого рычага, то увидим (в полном соответствии со СТО), что длины плеч рычага и величины векторов сил изменились. Они изменились так, что возник вращающий момент, стремящийся повернуть этот рычаг. Повернется ли рычаг?

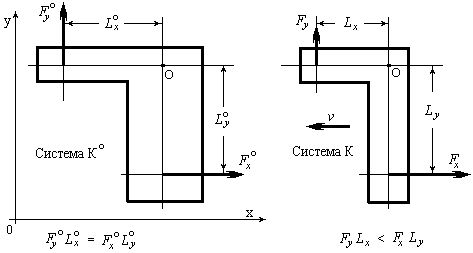
Рис. 2. Парадокс рычага

Мы не будем пересказывать беспомощное, противоречивое объяснение и давать ему критические замечания. Это сделано в Приложении 3 Части 6 работы [8]. Отметим лишь следующее. Как утверждают апологеты СТО, движущийся неуравновешенный рычаг вопреки законам механики не будет вращаться!

Зададим законные вопросы:

Предсказывая появление вращающего момента, действующего на движущийся рычаг, теория ошибается или же законы механики не «работают»?

Как можно определить: когда теория предсказывает правильный результат, которому можно доверять, а когда предсказываемый результат необходимо отбросить?

В электродинамике существует аналогичный парадокс («конвективный потенциал»). Пусть два неподвижных заряда уравновешены в собственной системе отсчета. Движущийся наблюдатель обнаружит, что помимо электрического поля возникает магнитное. Благодаря магнитному взаимодействию возникает вращающий момент, под действием которого система из этих зарядов должна повернуться.

В разделе 18.4 [9] читаем:

«Вращающий момент, предсказываемый теорией, реально существует для наблюдателя, движущегося относительно заряда со скоростью u. Он мог бы быть измерен, если бы не нужно было учитывать механические соображения. Мы уже говорили, что представление о «жестком» стержне несовместимо с теорией относительности».

Итак, теория относительности предсказывает появление вращающего момента. Опыты по обнаружению этого момента (эксперимент Траутона и Нобла) дали отрицательный результат. Чтобы «объяснить» несоответствие между теорией, экспериментом и здравым смыслом апологеты вытаскивают миф об «абсолютно жестких стержнях».

Теория, которая буквально «барахтается» в противоречиях, стыдливо именуемых «парадоксами», не может считаться научной теорией. Соответственно первый вариант объяснения релятивистских явлений должен быть отброшен. Члены гизбурго-кругляковской «Комиссии по борьбе с лженаукой и фальсификацией научных исследований» должны были бы проверить критические замечания в адрес СТО и давно признать, что СТО есть лженаучная теория. Но есть ли у них научное мужество или же для них «честь мундира», изрядно попачканного, превыше научной истины?

3. Вперед, к Ньютону!

Подведем краткие итоги. Первый вариант объяснений предполагает, что относительное движение влияет на пространство и время. Они теряют свою независимость и объединяются в 4-континуум, именуемый пространством Минковского. В результате мы имеем только две возможности для объяснения явлений.

Либо все инерциальные системы равноправны (принцип Галилея – Пуанкаре), но тогда в теории появляются логические противоречия. Такая теория не может считаться научной, т.е. является лженаучной.

Либо должна существовать выделенная (избранная) инерциальная система отсчета, по отношению к которой другие инерциальные системы неравноправны. Логические противоречия исчезают, но принцип Галилея – Пуанкаре «не работает».

Поскольку третьего не дано, рассмотрим второй вариант. Обратимся к объяснениям, опирающимся на независимое от времени и движения систем отсчета пространство и независимое от пространства и движения время. Чтобы проиллюстрировать особенности второго варианта вернемся к кинематическим парадоксам («замедление» времени и «сжатие» масштаба). По своей структуре и логике эти парадоксы подобны парадоксу «двух джентльменов».

Два джентльмена одинакового роста находятся в комнате по разные стороны от разделяющей их прозрачной перегородки. Они не подозревают, что прозрачная перегородка это большая двояковогнутая линза. Первый джентльмен обращается ко второму: «Уважаемый Сэр! Вы намного ниже меня. Вас мама в детстве плохо кормила?» Обиженный второй джентльмен возражает: «Я намного выше Вас. Вы, как я полагаю, из племени пигмеев?»

Все три парадокса аналогичны. Различие лишь в условии. В одном случае условием наблюдения явления выступает скорость относительного движения наблюдателей. Во втором – фокусное расстояние линзы. Эти различия не принципиальны. Помимо общей логики разрешения парадоксов, общим для трех парадоксов является также и свет, который доставляет наблюдателям искаженную информацию.

Рекомендуем скачать другие рефераты по теме: конспекты занятий в саду, реферат по педагогике.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки