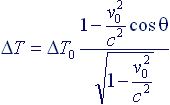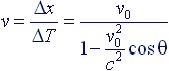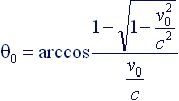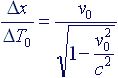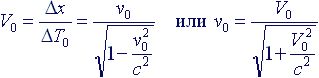Новое объяснение релятивистских явлений
Категория реферата: Рефераты по математике
Теги реферата: диплом управление, куплю диплом купить
Добавил(а) на сайт: Серпионов.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Парадокс джентльменов имеет очевидное объяснение. Каждый из них сравнивает свой действительный рост (характеристика сущности) с высотой мнимого изображения (явление) своего оппонента. Каждому из джентльменов кажется, что он «выше» своего оппонента. «На самом деле» их рост совершенно одинаков (сущность). Истолковывая явление как сущность, джентльмены совершают гносеологическую ошибку.
Тот же подход должен использоваться для анализа релятивистских парадоксов [11]. Анализ «замедления» времени показывает, что время едино и объективно (т.е. не зависит от выбора наблюдателем инерциальной системы отсчета). Во всех инерциальных системах отсчета оно течет в одном темпе, и нет никакой необходимости в процедуре «синхронизации» часов различных систем отсчета. Наблюдаемое замедление времени обусловлено стандартным эффектом Доплера. Отсюда следует решение «парадокса близнецов»: никакого «старения» неподвижного наблюдателя по отношению к движущемуся не будет.
То же заключение можно сделать и относительно «сжатия» масштаба. Этот эффект обусловлен изменением направления фронта световой волны в неподвижной системе по отношению к движущейся [11]. Как мы видели, некоторые ученые в объяснениях изложенных парадоксов фактически «скатывались» на эти позиции. Однако они не захотели или не смогли сделать следующий шаг: признать евклидовость пространства и единство времени во всех инерциальных системах отсчета. Гипноз авторитета оказался сильнее здравого смысла, да и философское невежество сыграло здесь не последнюю роль.
4. Лоренц ошибся, Эйнштейн повторил ошибку
Посмотрим теперь, к каким новым нестандартным результатам приводит признание евклидовости пространства и единства времени и их независимости от скорости перемещения наблюдателей.
В качестве примера рассмотрим материальный объект, который движется прямолинейно и равномерно относительно нас со скоростью v. Его траектория – прямая линия. Пусть на этом объекте установлена лампа, которая дает вспышки через равные интервалы времени ΔТо (система отсчета объекта).
Наблюдаемая прямолинейная траектория движения объекта будет для нас как бы разделена на равные интервалы длиной Δx (см. рис.3) точками вспышек. Измеряя интервалы времени ΔТ между соседними вспышками, мы увидим, что они зависят от угла наблюдения θ (эффект Доплера).
|
|
(4.1) |
где vo – лоренцевская скорость относительного движения инерциальных систем отсчета.
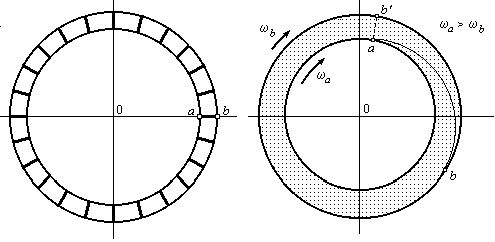
Рис. 3. Определение наблюдаемой скорости движения объекта
Разделим длину отрезка между вспышками Δx на наблюдаемый интервал времени ΔТ. Мы получаем выражение для величины кажущейся скорости v движения объекта. Эта скорость будет также зависеть от угла наблюдения θ.
|
|
(4.2) |
Если мы положим угол наблюдения θ равным 90о, то убедимся, что vo это скорость относительного движения систем отсчета, входящая в преобразование Лоренца. Нетрудно видеть, что при vo> (51/2–1) c/2 кажущаяся скорость v будет превышать скорость света в вакууме при малых углах наблюдения. Это легко объяснимо, поскольку кажущаяся скорость есть явление. Сам объект движется всегда с постоянной скоростью vo.
Теперь мы обращаем внимание читателя на другое немаловажное обстоятельство. Изменение масштаба вдоль направления движения, как и эффект Доплера зависят от угла наблюдения θ. Оказывается, что в преобразовании Лоренца существует такой угол наблюдения θо, при котором упомянутые выше эффекты не наблюдаются, т.е. частоту колебаний световой волны и наблюдаемый отрезок мы фиксируем без искажений. Назовем этот угол критическим. Если угол наблюдения меньше критического, тогда кажущаяся длина движущейся линейки будет длиннее покоящейся, а частота света выше. Если же угол наблюдения будет больше критического, движущаяся линейка будет наблюдаться короче неподвижной, а частота – ниже. Этот угол определяется из условия:
|
|
(4.3) |
Кажущаяся скорость движения объекта при критическом угле наблюдения будет равна
|
|
(4.4) |
С другой стороны, отношение Δx/ΔТо=Vo это классическая (галилеевская) скорость относительного движения двух инерциальных систем отсчета! Это обусловлено единством времени и евклидовостью пространства, общего для всех инерциальных систем. Величины Δx и ΔТо не искажены относительным движением инерциальных систем отсчета. Они соответствуют величинам, измеряемым при ньютоновском мгновеннодействии.
Ранее скорость Vo мы назвали галилеевской скоростью. Связь между лоренцевской скоростью относительного движения двух инерциальных систем отсчета и галилеевской скоростью относительного движения тех же систем задается соотношением:
|
|
(4.5) Рекомендуем скачать другие рефераты по теме: конспекты занятий в саду, реферат по педагогике. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |