Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата



Вычислив синус дуги γ, получим:

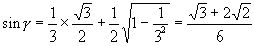
Т.к. сумма γ заключена на сегменте [-π/2; π/2], то

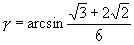
Пример №2. Представить дугу γ, рассмотренную в предыдущем примере, в виде арктангенса. Имеем:

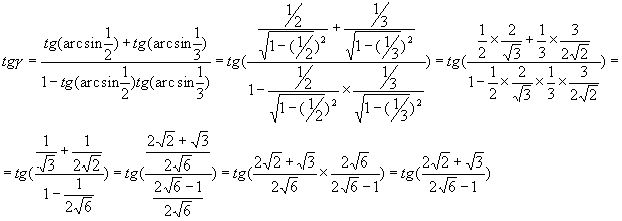
Откуда

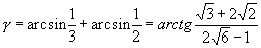
Пример №3. Представить посредством арктангенса сумму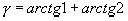

Решение: в данном случае (в отличие от предыдущего) дуга γ оканчивается во второй четверти, т.к. 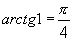, а 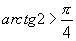. Вычисляем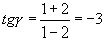

В рассматриваемом примере 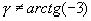, так как дуги γ и 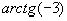заключены в различных интервалах,

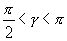, а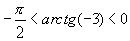

В данном случае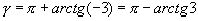

Пример №4. Представить дугу γ, рассмотренную в предыдущем примере, в виде арккосинуса.

Решение: имеем

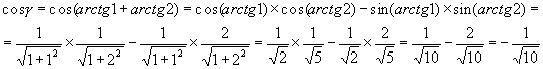
Обе дуги γ и 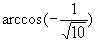расположены в верхней полуокружности и имеют одинаковый косинус, следовательно, эти дуги равны: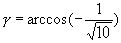

Так как суммы и разности любых аркфункций можно выражать при помощи произвольных аркфункций, то можно получать самые разнообразные формулы сложения. Однако все эти формулы выводятся при помощи однотипных рассуждений. Ниже в качестве примеров даются некоторые из формул сложения, по этим образцам можно получить аналогичные формулы в различных прочих случаях.

Формулы сложения аркфункций от положительных аргументов.

Пусть α и β – две дуги, заключенные в промежутке от 0 до π/2 (первая четверть):

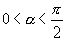, и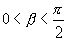

Сумма α + β ηаключена в верхней полуокружности 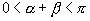, следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:

;

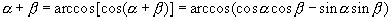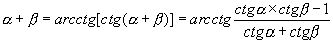
Разность α – β ηаключена в правой полуокружности: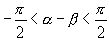

Следовательно, она может быть представлена в виде арксинуса, а также в виде арктангенса:

Рекомендуем скачать другие рефераты по теме: реферат по физкультуре, тарас бульба сочинение.

Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки