Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата



Вообще, если 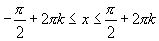, то

y=х-2πk

и если 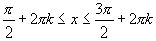, то

y=(π-х)+2πk

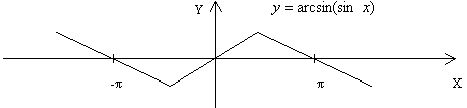
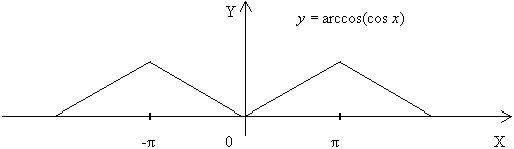
График функции 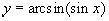представлен на рисунке. Это ломаная линия с бесконечным множеством прямолинейных звеньев.

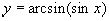
Рассмотрим функцию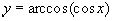

Согласно определению арккосинуса, имеем:

cos y = cos x, где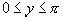

Областью определения данной функции является множество всех действительных чисел; функция периодическая, с периодом, равным 2π. Если значение Х принадлежит сегменту [0; π], то y = x. Если х принадлежит сегменту [π; 2π], то дуга 2π-х принадлежит сегменту [0; π] и 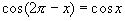, поэтому:

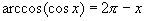
Следовательно, на сегменте [π; 2π] имеем y = 2π - x

Если х принадлежит сегменту [2π; 3π], то y = x - 2π

Если х принадлежит сегменту [3π; 4π], то y = 4π – x

Вообще, если 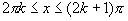, то y = x - 2πk

Если же 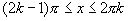, то y = -x + πk

Графиком функции 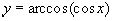является ломаная линия

Формулы сложения

Формулы сложения дают выражения для суммы или разности двух (или нескольких) аркфункций через какую-либо данную аркфункцию. Пусть дана сумма аркфункций; над этой суммой можно выполнить любую тригонометрическую операцию. (....) В соответствии с этим дуга-функция может быть выражена посредством любой данной аркфункции. Однако в различных случаях (при одних и тех же аркфункциях) могут получаться различные формулы, в зависимости от промежутка, в котором берется значение рассматриваемой аркфункции.

Сказанное пояснено ниже на числовых примерах.

Примеры.

Пример №1. Преобразовать в арксинус сумму

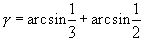
Решение: эта сумма является суммой двух дуг α и β, где

;

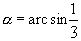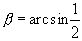
В данном случае 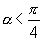(т.к. 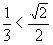, а следовательно, 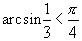), а также 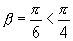, поэтому .

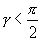Рекомендуем скачать другие рефераты по теме: реферат по физкультуре, тарас бульба сочинение.

Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки