Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Полиномы Чебышева - Эрмита.

Пусть многочлен (2) не имеет корней, тогда уравнение Пирсона (1) после переноса начала координат запишется в виде

,

тогда решение этого уравнения запишется в виде

    (6).

Линейным преобразованием независимого переменного

эта функция приводится с точностью до постоянного множителя  к весовой функции многочленов Чебышева – Эрмита, которая имеет вид

.

Поскольку умножение весовой функции на постоянную практически не изменяет ортогональные многочлены, то в формуле (6), как и в аналогичных нижеследующих формулах, не нарушая общности, можно полагать . В данном случае ортогональные многочлены с весом (6) выражаются через ортогональные многочлены Чебышева – Эрмита  по формуле

.

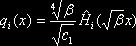В этом случае условие ортогональности запишется в виде:

если

Полиномы Чебышева - Лагерра.

Пусть теперь многочлен (2) имеет один корень. Тогда уравнение (1) представимо в виде

.

Тогда его решение запишется в виде

.

Многочлены, ортогональные с таким весом, можно рассматривать как обобщение многочленов Чебышева – Лагерра, ортогональных с весом

.

Причем и здесь можно выразить эти многочлены через многочлены Чебышева – Лагерра , а условие ортогональности будет:

           если

Полиномы Якоби.

Предположим, что многочлен (2) имеет два различных действительных нуля. Тогда , и уравнение Пирсона (1) представимо в виде

,

Рекомендуем скачать другие рефераты по теме: биология 6 класс, ответы 8 класс.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки