
Построение математических моделей при решении задач оптимизации
Категория реферата: Рефераты по математике
Теги реферата: реферат здания, бесплатные курсовые работы скачать
Добавил(а) на сайт: Erofeev.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 | Следующая страница реферата
S=AB*BC+p x /8
S=xy+ x p /8 (2)
Из (1),(2) следует, что
S(x)=-(p /8 +1/2)x +3x
Известно,что квадратный трехчлен принимает наибольшее значение при
x =-b/2a,т.е. x =12/(p +4), y= 6/ (p +4).
Ответ.Размеры окна 6/(p +4),12/(p +4).
Задача 6.На учебном полигоне произведен выстрел из зенитного орудия в вертикальном направлении не разрывающимся снарядом. Требуется определить наибольшую высоту подъема снаряда, если начальная скорость снаряда ν0 = 300 м/с. Сопротивлением воздуха пренебречь.
Решение.
Из курса физики известно, что путь s, пройденный телом при равноускоренном движении, изменяется в зависимости от времени по закону s = s0 + ν0 t + at2/ 2, где s0 – начальный путь, ν0 – начальная скорость, a – ускорение, t – время.
В рассматриваемом случае s =0,v =300 м/с, а=-5 м/с ,значит,S(t) = 300t – 5t2 .
Функция S(t) принимает наибольшее значение при
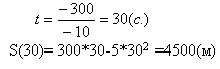
Наибольшая высота подъема снаряда равна 4500 м.
Как видно из примеров, решение экстремальных задач дает возможность установить более тесную межпредметную связь алгебры, геометрии и физики. При их решении можно приобрести не только математическую информацию, но и знания из курса физики.
Решение физических задач поучительно с точки зрения математики, так как можно показать тонкости тех или иных математических приемов в действии, в их практическом приложении.
В частности, эти задачи помогают осознать, что функция, заданная аналитической формулой, может выражать зависимости между реальными величинами в самых различных явлениях и процессах
Задача 7.Арка моста имеет форму параболы (высота 4 м, наибольшая ширина 20 м).
Составьте уравнение этой параболы.
Решение
Уравнение параболы в данном случае имеет вид y = ax2 + c. Для определения a и c подставим в этом уравнение координаты точек B и C (рис. 1), т.е.
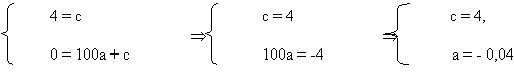
Парабола имеет вид: y = - 0,04x2 + 4.
4.Применение методов дифференциального исчисления при решении прикладных задач. Задача 8.Проектируется канал оросительной системы с прямоугольным сечением в 4,5 м2. Каковы должны быть размеры сечения, чтобы для облицовки стенок и дна пошло наименьшее количество материала?
Решение.
Пусть стенки канала имеют длину x м., а дно канала – y м.
Рекомендуем скачать другие рефераты по теме: решебник, дипломная работа проект.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 | Следующая страница реферата