Приближенное вычисление определенного интеграла при помощи квадратурной формулы Чебышева

КУРСОВАЯ РАБОТА студента 2-го курса: Полякова Е.В.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

ГОСУДАРСТВЕННЫЙ ХИМИКОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Днепропетровск 2000г.

1. Общая постановка и анализ задачи.

1.1. Введение.

Требуется найти определенный интеграл

 I =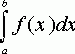

по квадратурной формуле Чебышева.

Рассмотрим, что представляет из себя вообще квадратурная формула, и как можно с ее помощью вычислить приближенно интеграл.

Известно, что определенный интеграл функции  типа 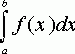 численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис.1).

Рис. 1. Криволинейная трапеция.

Если f(x) непрерывна на отрезке [a, b], и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по, известной всем, формуле Ньютона - Лейбница

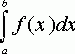= F(b) - F(a)

 где

 F’(x) = f(x)

 Однако во многих случаях F(x) не может быть найдена, или первообразная получается очень сложной для вычисления.

Кроме того, функция часто задается таблично. Поэтому большое значение приобретает приближенное и в первую очередь численное интегрирование.

 Задача численного интегрирования состоит в нахождении приближенного значения интеграла 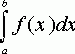по заданным или вычисленным значениям подинтегральной функции f(x) в некоторых точках ( узлах ) отрезка [ a, b].

 Численное определение однократного интеграла называется механической квадратурой, а соответствующие формулы численного интегрирования - квадратурными .

 Заменяя подинтегральную функцию каким-либо интерполционным многочленом, мы получим квадратурные формулы вида

 

  

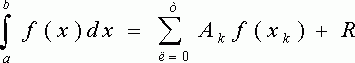
 где

 xk - выбранные узлы интерполяции;

 Ak - коэффициенты, зависящие только от выбора узлов, но

 не от вида функции (k=0,1,2,........, n).

 R - остаточный член, или погрешность квадратурной формулы.

 Отбрасывая остаточный член R, мы совершаем погрешность усечения.

Рекомендуем скачать другие рефераты по теме: реферат сша, реферат группы.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки