Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

1.3 Формула трапеций и средних прямоугольников.

Заменим дугу АВ стягивающей ее хордой, получим прямолинейную трапецию аАВb, площадь которой примем за приближенное значение интеграла

B

y

 0 a b x

 рис 1.3.1 Криволинейная трапеция

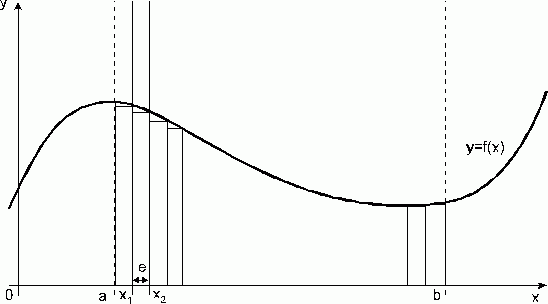
Рис. 1.3.2. Метод трапеций.

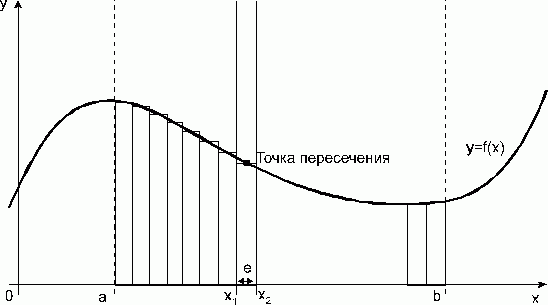
Рис. 1.3.3. Метод средних прямоугольников.

По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей —

для метода трапеций:

,

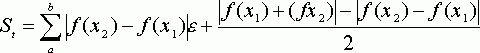для метода средних прямоугольников:

.

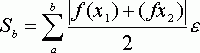1.4. Общая формула Симпсона (параболическая формула)

Пусть n=2m есть четное число и yi=f(xi) (i=0,1,2...n) - значения функции y=f(x) для равноотстоящих точек а=x0,x1, ... ,xn=b с шагом

  

Применив формулу Симпсона к каждому удвоенному промежутку [x0,x2], [x2,x4] ... [x2m-2,x2m] длины 2h и введя обозначения

s1=y1+y2+ ... +y2m-1

s2=y2+y4+ ... +y2m

получим обобщенную формулу Симпсона:

 

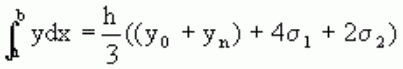
Остаточный член формулы Симпсона в общем виде:

 

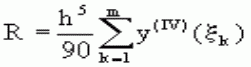
Рекомендуем скачать другие рефераты по теме: реферат сша, реферат группы.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки