Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата



х4=0; из трех чисел х1 , х2, х3 хотя бы одно отлично от нуля; отношение х1/х2/х3 равно отношению m/n/p, где m,n,p - параметры уравнения любой прямой, проходящей через точку МҐ (х -х0 ) / m=(y -y0) ) / n=(z -z0 ) / p.

Аналогично уравнению прямой в однородном виде (u1 x1+u2 x2+u3 x3+u4 x4=0) можно записать уравнение плоскости в таком же виде: Ax+By+Cz+D=0 ,Ax1+Bx2+Cx3+Dx4=0 или u1x1+u2x2+u3x3+u4x4=0

Вершины координатного тетраэдра (пять точек): Ґx , Ґy , Ґ z , 0, E

A1 (1,0,0,0) , A2 (0,1,0,0) , A3 (0,0,1,0) , A4 (0,0,0,1) , E (1,1,1,1) ..

Аналитическое представление проективных преобразований (отображений)

1. Сначала рассмотрим проективные отображения плоскости на плоскость. Что такое проективное преобразование (отображение)? Очевидно, это такое отображение, при котором сохраняются проективные свойства объекта, например такое, как разделенность двух пар точек и гармонически сопряженные пары точек. Пусть М/=f(M) - проективное отображение (М - прообраз в исходной плоскости a, М/ - образ в преобразованной плоскости a/). Можно доказать, что и обратное отображение М=f-1 (M/) тоже является проективным, т.е. это взаимно однозначное отображение (биективное).Т.к. все проективные свойства опираются на свойства разделенности и гармонического сопряжения двух пар четырех соответствующих элементов (точек, прямых в пучке в одной плоскости), то существует теорема , по которой проективное отображение одной плоскости в другую однозначно определяется заданием четырех пар соответствующих по отображению точек, при условии, что никакие три из них не лежат на одной прямой. Показывается, что простейшим таким отображением является линейное отображение вида М(х1 ,х2 ,х3) ® М/ (s/x1/ , s/x2/ , s/x1/ )

s/x1/ =c11 x1+c12 x2+c13 x3 Числа сi k определяют матрицу такого преобразования,

(1) s/x2/ =c21 x1+c22 x2+c23 x3 причем для взаимной однозначности отображения

s/x3/ =c31 x1+c32 x2+c33 x3 необходимо, чтобы определитель матрицы № 0. По указанному выше замечанию преобразование (1) однозначно определено, если заданы четыре пары соответствующих точек М1 , М2 , М3 , М4 ® М/1 , M/2 , M/3 , M/4 . Более того, всякое линейное отображение вида (1) , определитель которого отличен от нуля, есть проективное отображение. Проективные преобразования составляют группу: это значит, что существует тождественное проективное преобразование (единичное) , обратное к заданному, а также произведение двух проективных преобразований есть снова проективное преобразование. Пусть заданы в плоскости a четыре точки Мk (k=1,2,3,4) с проективными координатами х1 k , х2 k , х3 k , никакие три из которых не лежат на одной прямой, и четыре точки М/k (k=1,2,3,4) в плоскости a/ с проективными координатами x/1 k , x/2 k , x/3 k , также никакие три из которых не лежат на одной прямой . Надо показать, что из линейных преобразований:

1)

s/kx/1 k =c11 x1 k+c12 x2 k+c13 x3 k

s/kx/2 k=c21 x1 k+c22 x2 k+c23 x3 k c №0

s/kx/3 k=c31 x1 k+c32 x2 k+c33 x3 k

можно однозначно найти 9 параметров сi k и 3 параметра s/k (k=1,2,3) , а s/4 всегда можно выбрать равным единице.

2) В трехмерном пространстве:

Каково бы ни было проективное отображение М/=f (M) точек пространства I на пространство I/ , проективные однородные координаты x/1 , x/2 , x/3 , x/4 точки М/ выражаются через проективные однородные координаты х1 , х2 , х3 , х4 точки М с помощью линейных соотношений:

s/kx/1 k=c11 x1 k+c12 x2 k+c13 x3 k+c14 x4 k

s/kx/2 k=c21 x1 k+c22 x2 k+c23 x3 k+c24 x4 k

(2) s/kx/3 k=c31 x1 k+c32 x2 k+c33 x3 k+c34 x4 k

s/kx/4 k=c41 x1 k+c42 x2 k+c43 x3 k+c44 x4 k

с постоянными коэффициентами сi k и при этом определитель матрицы такого преобразования D= с =(сi k) №0.

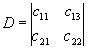3) Аналогичные определения существуют при проективном отображении прямой a на прямую a/. Если М/ - точка на прямой а/ с однородными координатами х/1 , x/2 ,и точка М - на прямой а с однородными координатами x1 , x2 ,то проективное преобразование М/ = f (M) однозначно определяется из соотношений:

s/x/1 = c11 x1+c12 x2

s/x/2= c21 x1+c22 x2 и

Часто бывает удобным использовать проективные преобразования в неоднородных координатах.

Для прямой : Если х1 , х2 - однородные координаты точки М на прямой ,то х=х1 / x2 - число, являющееся неоднородной координатой точки М на этой прямой . Пусть задано проективное преобразование прямой а на прямую а/ . Значит, существуют соотношения :

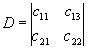
Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки