Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

sx/1 = c11 x1+c12

sx/2 =c21 x1+c22 x2

Разделим почленно первое равенство на второе :

sx/1 /sx/2 =(c11 x1+c12 x2) / (c21 x1+c22 x2) , учитывая , что x/=x/1 / x/2 , и x=x1 / x2 .

Преобразуем

x/=(c11 x+c12)/ (c21 x+c22) , введя новые обозначения : a=c11 , b=c12 , g=c21 , d=c22

x/=(ax+b) / (gx+d) - т.е. в неоднородных координатах проективное преобразование выражается дробно - линейной функцией. ad -bg №0

Для плоскости : Однородные координаты точки М - х1 , х2 , х3 , неоднородные : x=x1 / x3 ,y=x2 / x3 .

Формулы проективного преобразования в неоднородных координатах :

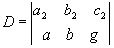x/=(a1 x+b1 y+c1) / (ax+by+ g) , a1 b1 c1 y/=(a2 x+b2 y+c2) / (ax+ by+ g) где

В трехмерном пространстве :

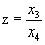
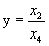
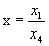
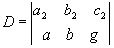Однородные координаты (x1 , x2 , x3 , x4)) .

Неоднородные координаты

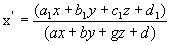
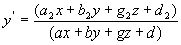
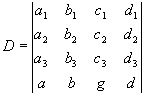
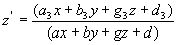
Рассмотрим подробнее проективные преобразования одномерных многообразий, здесь можно ограничится случаем преобразования прямой на прямую. Как установили ранее, в неоднородных проективных координат на прямой это преобразование имеет вид дробно-линейной функции (1) х/= a х+ b / g х+d , причем, чтобы существовало обратное проективное преобразование, необходимо, чтобы величина ad - bg № 0. Запишем преобразование (1) в виде функции х/= f(x).

Пусть данное отображение применяется последовательно два раза: х/= f(x), x//= f(x/)= f(f(x)). Тогда, если для любого элемента х одномерного многообразия (на прямой) выполняется соотношение x//= f(x/)= х (то есть дважды преобразованный возвращается в себя) , то такое проективное отображение называется инволюционным или инволюцией. Инволюция характеризуется еще и тем, что x= f(x/), т. е. обратное отображение х/= х совпадает с исходным х= х/. Найдем условие на коэффициенты в (1), при которых проективное отображение является инволюцией. Для этого из (1) выразим х через х/ : (g x /- a )x= - d x/ + b Ю x= - d x/+b / g x /- a (2). Из сравнения (1) и (2) видно, что отображения одинаковы тогда, когда либо:

а) d =- a , g, b - любые

б) d = a, g = b = 0 - но это тождественное отображение, которое исключим из рассмотрения.

Таким образом, из случая а) вытекает форма инволюционого проективного отображения х/= a х+ b /g х- в , где -a2- bg № 0 обозначим D = -a2- bg

Неподвижной точкой любого отображения называется точка, остающаяся неизменной после отображения. Для инволюции это означает , что х =х/= a х+ b /g х- в .

Решим последнее уравнение относительно х (3) g х2-2 a х- b= 0 - квадратное относительно х.

Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки