Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата



Матрицы проективных преобразований.

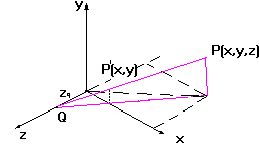
Представим перспективную проекцию объекта как проективное преобразование с центром проекции на оси z (на расстоянии zq от начала координат). Пусть плоскостью проекции является координатная плоскость XOY

P(x,y,z)-точка объекта , P/(X,Y)-её проекция из центра Q. Известно, что координаты точки-проекции P/ есть X=x/(1-z/zq) , Y=y/(1-z/zq) (*)

Однородные координаты точки P (x,y,z,1) - P/(x/,y /,z/,w /) ,w №0.

Преобразование (*) может быть выражено через матрицу проективных преобразований в однородных координатах:

Неоднородные координаты точки P/

получаем отсюда : X=x/(1-z/zq ) ,

Y=y/(1-z/zq ) ,Z=0

Найдём проекцию бесконечно удаленной точки на оси Z - $ однородные координаты (0,0,1,0).

Вместо МПр возьмем матрицу полного проективного преобразования (без проецирования на плоскость XOY).

Неоднородные координаты проекции этой точки (0 ,0 , -zq )

Если взять семейство параллельных оси z прямых, то после такого проективного преобразования каждая из них пройдет через указанную точку (0,0,-zq ) на оси z .Поэтому эту точку называют точкой схода.

Аналогично, матрицы

описывают проективные преобразования с точками схода на оси OX и OY. Это все преобразованные с одной точкой схода.

Матрица

преобразование с двумя точками

А это с тремя схода

Групповые свойства проективных преобразований

Группа - есть совокупность объектов произвольной природы, которые называются элементами группы а обозначается символами a, b, c, ..., удовлетворяющая требованиям следующих аксиом:

1. С каждой парой элементов совокупности, взятых в определённом порядке, сопоставлен по определённому закону некоторый третий элемент этой же совокупности.

Символически это записывают так c=ab, элемент c называется произведением (композицией) элементов a и b. Иначе: композиция двух любых элементов группы даёт элемент, принадлежащий этой же группе.

2. Закон ассоциативности: Каковы бы ни были три элемента группы a, b, c, всегда имеет место соотношение (ab)c=a(bc)

3. Существует такой элемент e , что для любого элемента a группы выполняется ae=a.

Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки