Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Утверждение требует проверки только когда лучи [OA) и [OB) совпадают. В этом случае |OA| ¹ |OB| и поэтому |OA¢| ¹ |OB¢|. Приходим к неравенству A¢ ¹ B¢.

II. Все точки окружности w(O,R) при инверсии invOR остаются неподвижными. Внутренние точки круга с границей w(O,R) переходят во внешние, а внешние - во внутренние.

Первая часть утверждения очевидна, а вторая следует из замечания: если

|OA| < R, то |OA¢| = R2/|OA| > R.

III. Если A¢ = invOR(A), то A = invOR(A¢). Для произвольных фигур F и F¢ из условия F¢ = invOR(F) также следует F = invOR(F¢).

IV. Треугольники DAOB и DA¢OB¢ подобны. При этом ÐOBA = ÐOA¢B¢.

Достаточно заметить, что эти треугольники имеют общий угол, а из равенства |OA|·|OA¢| = R2 = |OB|·|OB¢| следует равенство отношений |OA|/|OB¢| = |OB|/|OA¢|. Обратите внимание, что в отличие от подобия, пропорциональность связывает стороны [OA] и [OB¢], [OB] и [OA¢], а не [OA] и [OA¢], [OB] и [OB¢]. Из подобия получаем ÐOBA = ÐOA¢B¢.

V.

|A¢B¢| =   |AB|

|OA|·|OB|                         ·R2.

Действительно, по свойству IV имеем

|A¢B¢| =   |AB|·|OA¢|

|OB|        =          |AB|

|OA|·|OB|                          ·R2.

VI. Прямая a, проходящая через центр инверсии, отображается в себя. Если же O Ï a и A - основание перпендикуляра из точки O на прямую a (рис. 4), то образом прямой a будет окружность w1, построенная на отрезке [OA¢] как на диаметре (A¢ = invOR(A)).

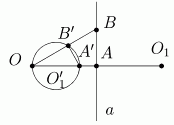
Рис. 4

Для доказательства этого свойства рассмотрим произвольную точку B прямой a. По свойству IV ÐOB¢A¢ = ÐOAB = 90°. Следовательно точка B¢ лежит на окружности с диаметром [OA¢]. Удивление от такого неожиданного действия инверсии на произвольную прямую пройдет, если принять в расчет бесконечно удаленную точку. Каждая прямая проходит через ¥. Поэтому переход ¥ в точку O заставляет концы прямой сжиматься к точке O. Следующее свойство позволяет определить центр окружности, которая является образом прямой из свойства VI.

VII. Пусть w1 = invOR(a). Обозначим через O1 = Sa(O), где Sa - осевая симметрия с осью a (рис. 4). Тогда центром окружности w1 является точка O1¢ = invOR(O1).

Сохраняя принятые в предыдущем свойстве обозначения, имеем |OO1| = 2|OA|. Подставляя это в равенство |OA|·|OA¢| = R2 = |OO1|·|OO1¢| получаем |OO1¢| = |OA¢|/2. Поэтому точка O1¢ является серединой отрезка [OA¢].

VIII. Окружность w1(O1,r), проходящая через центр инверсии, отображается на некоторую прямую a. Более того, если A - конец диаметра, проходящего через O и O1 (A ¹ O), то прямая a проходит через точку A¢ = invOR(A) и перпендикулярна прямой (OO1).

Справедливость этого свойства сразу следует из свойств III и VI.

IX. Окружность w1(O1,r1), не проходящая через центр инверсии, отображается при invOR на некоторую окружность w2(O2,r2). Точнее, если точки A и B являются концами диаметра, лежащего на прямой (OO1) (рис. 5), то отрезок [A¢B¢] является диаметром окружности w2 (A¢ = invOR(A), B¢ = invOR(B)).

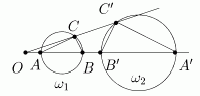
Рис. 5

Рекомендуем скачать другие рефераты по теме: реферат россия скачать, пример реферата.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки