Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

|X¢Y¢| = |XY|

|OX|·|OY|           ·r2 =     2Rr2

|R-d|·|R+d|          =          2Rr2

R2-d2      .

Учитывая, что |X¢Y¢| = 2R¢, где R¢ - радиус окружности invOr(w1), получаем формулу

R¢ =        Rr2

R2-d2                    .

Возвращаясь к образу описанной окружности при инверсии относительно w(O,r), имеем

   r

2 =          Rr2

R2-d2          ÞR2-d2 = 2RrÞd2 = R2-2Rr.

Закончим этот параграф одним совершенно неожиданным результатом. Сначала напомним некоторые определения и факты. Окружностью Эйлера треугольника ABC называется окружность, проходящая через середины его сторон. На этой окружности также лежат основания высот DABC и середины трех отрезков, соединяющих ортоцентр этого треугольника (т.е. точку пересечения его высот или их продолжений7) с вершинами. Поскольку на окружности Эйлера лежат девять точек, естественно связанных с треугольником ABC, ее называют еще окружностью девяти точек. Вневписанной окружностью треугольника ABC называется окружность, касающаяся стороны этого треугольника и продолжений двух других его сторон. В следующей лемме перечисляются некоторые свойства вневписанной окружности.

Лемма 1. Пусть |AB| = c, |AC| = b, |BC| = a, p - полупериметр DABC, O1 и Oa - центры вписанной (w1) и вневписанной (wa) окружностей (рис. 13), r1 и ra - их радиусы, X и Xa - точки касания этих окружностей со стороной [BC], K и L - с прямой (AC), M и N - с прямой (AB). Пусть также (B1C1) - общая внутренняя касательная к w1 и wa, отличная от (BC). Тогда

|AL| = p;

|AK| = p-a, |CK| = p-c, |BX| = p-b;

|BX| = |CXa|;

|BC1| = |B1C| = |b-c|;

pr1 = ra(p-a);

r1ra = (p-b)(p-c).

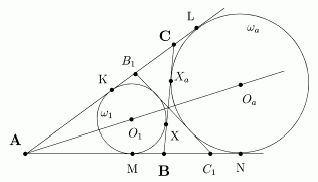
Рис. 13

Доказательство. 1) Следует из 2|AL| = |AL|+|AN| = (|AC|+|CXa|)+(|AB|+|BXa|) = 2p.

2) Первое равенство получается из 2|AK| = |AK|+|AM| = (|AC|-|CX|)+(|AB|-|BX|) = 2p-2a. Остальные доказываются аналогично.

3) Из 2) и 1) имеем |BX| = p-b = |AL|-|AC| = |CL| = |CXa|.

4) При симметрии относительно биссектрисы [AOa) угла ÐBAC окружности w1 и wa остаются неподвижными и отрезок [BC] одной внутренней касательной переходит в отрезок [B1C1] другой внутренней касательной. Отсюда |BC1| = |B1C| и |C1N| = |CL|. Из последнего равенства в предположении b > c получаем |BC1| = |AN|-|AB|-|CL| = p-c-(p-b) = b-c.

Рекомендуем скачать другие рефераты по теме: реферат россия скачать, пример реферата.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки