Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Для доказательства рассмотрим произвольную точку C окружности w1 и покажем, что C¢ = invOR(C) Î w2. Из свойства IV имеем равенства ÐOCA = ÐOA¢C¢ и ÐOCB = ÐOB¢C¢. Поэтому ÐA¢C¢B¢ = ÐOB¢C¢- ÐOA¢C¢ = ÐOCB-ÐOCA = 90°. Следовательно C¢ Î w2.

Переходит ли центр O1 в центр образа w2, точку O2? Никогда (убедитесь в этом с помощью прямых вычислений, т.е. докажите, что O1¢ = invOR(O1) не может быть серединой [A¢B¢]). Этот "недостаток" инверсии с лихвой компенсируется замечательным ее свойством сохранять величину угла. Напомним, что угол между пересекающимися окружностями по определению равен углу между касательными к этим окружностям в точке их пересечения. Аналогично определяется и угол между пересекающимися прямой и окружностью. Рассмотрим частный случай: для двух касающихся окружностей w1 и w2 определим величину угла между invOR(w1) и invOR(w2). Вид образов invOR(w1) и invOR(w2) во многом зависит от положения точки O относительно окружностей w1 и w2. Так, если O Ï w1Èw2, то из свойств I и IX получаем, что invOR(w1) и invOR(w2) являются касающимися окружностями. Если же O лежит только на одной из окружностей, например на w1, то из свойств I, VIII и IX получим касающиеся прямую invOR(w1) и окружность invOR(w2). И, наконец, если O совпадает с точкой касания окружностей, то invOR(w1) и invOR(w2) являются параллельными прямыми (величина угла между параллельными прямыми по определению равна нулю). Итак, в каждом из случаев, величина угла между invOR(w1) и invOR(w2) равна нулю. Аналогично можно установить, что если прямые a и b параллельны, то величина угла между invOR(a) и invOR(b) также равна нулю.

X. Инверсия сохраняет величину угла между прямыми, пересекающимися окружностями, пересекающимися прямой и окружностью.

Докажем сначала, что для любых прямых угол Ða,b совпадает с углом между invOR(a) и invOR(b). Утверждение очевидно, если прямые проходят через точку O. Пусть теперь O Î a и O Ï b (рис. 6). Обозначим через w1 окружность, в которую переходит прямая b, и через b1 - касательную к w1 в точке O. Так прямые b и b1 перпендикулярны одному и тому же диаметру, то они параллельны. Поэтому угол между a и w1, равный по определению углу между a и b1, совпадает с углом Ða,b. Рассуждения аналогичны и в случае, когда O Ï aÈb (надо рассмотреть касательные к окружностям invOR(a) и invOR(b) в точке O).

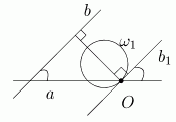
Рис. 6

Поскольку угол между окружностями и между прямой и окружностью определялся через касательные, то доказательство остальных двух утверждений легко сводятся к случаю сохранения угла между прямыми.

Основой решения целого ряда геометрических проблем является удачное применение того или иного преобразования плоскости. При этом мы считаем использование какого-либо преобразования удачным, если образы рассматриваемых фигур поддаются простому геометрическому анализу. В задаче Фаньяно1, например, стороны треугольника наименьшего периметра получаются из отрезка прямой серией осевых симметрий. При отыскании точки Ферма2 похожая идея реализуется с помощью поворота на 60°. В следующих параграфах попробуем выяснить насколько способность к упрощению свойственна инверсии. Этот параграф закончим решением проблемы A.

Решение A. Обозначим через A, B, C, и D соответственно точки касания w1Çw2, w2Çw3, w3Çw4 и w4Çw1. Сделаем инверсию с центром в O = A относительно окружности некоторого радиуса R. По свойству VIII и IX получим пару параллельных прямых a = invOR(w1), b = invOR(w2) и пару касающихся окружностей w3¢ = invOR(w3) и w4¢ = invOR(w4) (рис. 7).

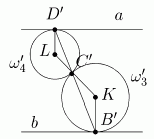
Рис. 7

Нетрудно заметить, что точки касания исходных окружностей, за исключением точки A (которую инверсия забросит в бесконечность), отобразятся в точки касания образов. Докажем теперь, что B¢, C¢ и D¢ лежат на одной прямой. Так как (KB¢)||(LD¢), то ÐB¢KC¢ = ÐC¢LD¢. Отсюда следует равенство ÐKC¢B¢ = ÐLC¢D¢ (DKC¢B¢ и DLC¢D¢ являются равнобедренными), поэтому B¢, C¢ и D¢ лежат на одной прямой. Обозначим эту прямую через c и подействуем на нее снова инверсией invOR. Ее образ - это окружность invOR(c), которая проходит через центр инверсии, точку A, а также через точки B = invOR(B¢), C = invOR(C¢) и D = invOR(D¢).

Геометрия Мора-Маскерони

Теория построения одним циркулем получила свою известность благодаря книге "Геометрия циркуля"(1797 г.) Лоренцо Маскерони3. Значительно позже в одном из букинистических магазинов была обнаружена книга датского математика Георга Мора "Датский Евклид", датированная 1672 годом! Обе книги содержат основной результат геометрии циркуля:

Теорема Мора-Маскерони. Все построения, выполненные с помощь циркуля и линейки, могут быть проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).

Для доказательства этой теоремы достаточно научиться находить только с помощью циркуля пересечения двух прямых, прямой и окружности, что и составляет проблему D. Сначала рассмотрим решения задач B и C, которые носят вспомогательный характер.

Решение B. Чтобы разделить отрезок [AB] на n равных частей, сначала увеличим его в n раз, т.е. найдем точку C, что |AC| = n|AB|. А затем построим точку C¢ - образ точки C при инверсии относительно окружности w(A,|AB|). Из соотношения |AC|·|AC¢| = |AB|2 получаем |AC¢| = |AB|/n. Все указанные построения можно выполнить только с помощью циркуля (для этого даже не нужна прямая (AB)).

Решение C. Выберем произвольную точку O окружности w1(X,r), центр X которой нам нужно определить (рис. 8).

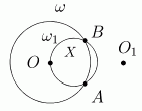
Рис. 8

Из точки O проведем произвольную окружность w(O,R) так, чтобы она пересекала исходную окружность w1. Обозначим точки пересечения wÇw1 через A и B. Куда перейдет прямая (AB) при инверсии invOR? Конечно же в w1, поскольку точки A и B остаются неподвижными (свойства II и VI). По свойству VII центр invOR((AB)) (т.е. центр w1) является образом точки S(AB)(O) при invOR. Из этих рассуждений следует цепочка необходимых построений. Сначала находим точку O1 = S(AB)(O), симметричную O относительно прямой (AB) (школьная задача). А затем строим образ точки O1 при invOR, он и будет искомым центром. Все указанные построения выполняются только с помощью циркуля.

Решение D. Опишем поиск пересечения двух прямых только с помощью циркуля. Пусть даны точки A, B, C и D (рис. 9).

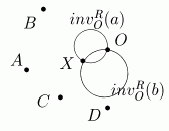
Рис. 9

Выберем точку O так, чтобы она не лежала на прямых a = (AB) и b = (CD). При инверсии invOR прямые a и b должны перейти в окружности invOR(a) и invOR(b), а их точка пересечения отобразится в точку пересечения окружностей invOR(a) и invOR(b), отличную от точки O (свойства VI и I). Теперь необходимые построения становятся очевидными: с помощью свойства VII строим окружности invOR(a) и invOR(b), находим точку пересечения этих окружностей - точку X, и снова действуем инверсией уже на точку X. Точка Y = invOR(X) является искомой. Пересечение прямой и окружности находится похожим образом.

Теперь терема Мора-Маскерони следует из решений задач B, C и D.

Рекомендуем скачать другие рефераты по теме: реферат россия скачать, пример реферата.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки