Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Теперь повернем оба наших аектора так, чтобы вектор A совпал с одной из осей. В этом случае проекция вектора B на вектор A определяется особенно просто - надо взять компоненту, соответствующую оси X, и эта величина и будет проекцией.

Для того, чтобы этот метода работал в произвольно взятой системе гиперкомплексных чисел Кэли - Диксона, выберем в качестве такой целевой оси для доворота действительную ось, поскольку в любой алгебре Кэли - Диксона определена действительная компонента.

Отметим тот факт, что поворот должен осуществляться в плоскости, проходящей через действительную ось и мы можем использовать механизм скалярно - пространственных поворотов, описанный в работе [2]. В случае использования алгебр, коммутативных по умножению, поворот может быть осуществлен так же, как на обычной комплексной плоскости, путем простого умножения на оператор поворота.

3. Скалярная проекция гиперкомплексных чисел.

Будем искать оператор поворота в виде

Будучи примененным к вектору A, этот поворот должен дать действительное число:

Несложно видеть, что этому уравнению удовлетворяет решение

Или, иначе говоря, сам вектор A и задает оператор поворота, на который следует его повернуть, чтобы получить действительное число.

Применив этот оператор поворота к вектору B, получим:

И для того, чтобы получить проекцию, следует взять действительную часть вектора B’ и провести соответствующую нормировку, поскольку указанным поворотом мы исказили величину модуля вектора B.

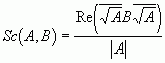
К числу весьма важных свойств скалярного произведения относится:

Поэтому, стремясь найти для гиперкомплексных чисел полную аналогию скалярному произведению, мы не будем использовать нормировок. В этом случае определенное выше правило выглядит как:

И для случая A = B переходит в

Перечислим еще раз свойства скалярного произведения в классическом варианте и найдем соответствия им в случае гиперкомплексных чисел:

1) , причем (x,x) только при x = 0

2) (x,y) = (y,x)

Рекомендуем скачать другие рефераты по теме: курсовые работы, реферат бесплатно на тему.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки