Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Французский епископ Николь Орем (1323-1382) рассматривал «дробно – рациональные отношения», соответствующе современным степеням a½, a¼, a3/2 и т.д., сформулировал правила операций с этими отношениями типа ,    ,         ,               ,           

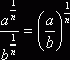Орем вплотную подошел к понятию иррационального показателя. Он доказал расходимость гармонического ряда 1 + +++…

Выдающимся алгебраистом своего времени стал монах-францисканец Лука Пачоли (ок. 1445 – ок.1514) близкий друг Леонардо да Винчи, работавший профессором Математики в университетах и различных учебных заведениях Рима, Болоньи, Неаполя, Флоренции, Милана и других городов.

Он ввел «алгебраические буквы» (caratteri algebraici), дал обозначения квадратному и кубическому корням, корню четвертой степени; неизвестную х он обозначал со (cosa – вещь), х2 – се (censo - квадрат, от латинского census), х3 – cu (cubo), x4 – се. се. (censo de censo), x5 – р°г° (primo relato – «первое relato», x6 – р°г° х – се. cu. (censo de «второе relato»), х8 – ce. ce. ce. (de censo), x9 – cu. cu. (cubo de cubo), x10 – ce. p°r° (censo de primo relato), x13 – 3°r° (tersio relato - «третье relato») и т. д.; свободный член уравнения – n° (numero – число). Как видим, некоторые степени Пачоли получал мультипликативным способом с помощью показателей 2 и 3 (х4 = х2×2 , х6 = х2×3, х9 = х3×3 и т. д.), а в случаях, когда так не получалось, пользовался словом relato (например, при образовании х5, х7, х11 и т. д.). Специальными символами Пачоли обозначил вторую неизвестную и ее степени. Для обозначения операции сложения он воспользовался знаком  (plus – больше), для обозначения вычитания – знаком  (minus – меньше). Он сформулировал правила умножения чисел, перед которыми стоят знаки и .

Раздел «Суммы», посвященный алгебраическим уравнениям, Пачоли закончил замечанием о том, что для решения кубических уравнений х3 + ах = b и х3 + b = ах «искусство алгебры еще не дало способа, как не дан еще способ квадратуры круга».

Некоторый шаг в совершенствовании алгебраической символики сделал бакалавр медицины Н. Шюке (ум. ок. 1500 г.), который в книге «Наука о числах в трех частях» изложил правила действий с рациональными и иррациональными числами и теорию уравнений. Для сложения и вычитания он вслед за Пачоли пользовался знаками  и , причем, знак  служил и для обозначения отрицательного числа. Неизвестную величину он называл premier («первое число»), а ее степени – вторыми, третьими и т. д, числами. Записи степеней неизвестной у Шюке лаконичны. Например, современные символы 5, 5ж, 5х, 5х2, 5х3 у него выглядели бы так: 5°, 51, 52, 53. Вместо равенства 8х3×7х-1 = 56х2 Шюке писал: «83, умноженное на 71×, дает 562». Таким образом, он рассматривал и отрицательные показатели. Относительно свободных членов уравнения Шюке указывал, что эти числа «имеют имя нуль».

Значительного успеха в совершенствовании «алгебраических букв» Луки Пачоли достигли немецкие алгебраисты – «коссисты». Они вместо  и ввели знаки + и –, знаки для неизвестной, и ее степеней, свободного члена.

XVI в. в алгебре ознаменовался величайшим открытием – решением в общем виде уравнений третьей и четвертой степеней.

Спицион дель Ферро в 1506 г. нашел решение кубического уравнения вида

 x3 + ax = b a,b >0. (1)

Чуть позже Тарталья указал решение этого же уравнения в виде х = - , где u – v = b, uv = , откуда u и v находятся как корни квадратного уравнения.

Также он нашел решение уравнения x3 = ax + b a,b >0 (2)

в виде х = + , где u + v = b, uv = .

Уравнение же x3 + b = ax a,b >0 можно решить с помощью уравнения (2).

В те времена предпочитали избегать отрицательных корней и задачи, сводящиеся к отрицательным корням уравнения (2), преобразовывали так, чтобы они приводили к положительным корням уравнения (3). Лишь Кардано позже осознал выгоду рассмотрения отрицательных корней.

Почему рассматривались только уравнения вида (1) и (2)? На этот вопрос ответ дал Кардано.

Чтобы разобраться в нем, рассмотрим полное уравнение третьей степени.

y3 + ay2 + by + c = 0.

Не следует думать, что Тарталья и Кардано писали такие уравнения. Нет, так стали поступать гораздо позже. Записывать все члены уравнения в одной части, приравнивая к одной части, начал Декарт. Да и символики не было, пользовались прообразами символов и словами. Уравнение x3 + ax = b записывалось примерно так: «куб» (х3) некоторое количество (а) «вещей» (х) равно данному «числу» (b). Понять можно, но оперировать сложно.

Полное уравнение можно преобразовать в неполное, не содержащее члена с квадратом неизвестной. Сделаем замену y = x + a и подставим в уравнение; получим х3 + (3a + а)х2 + (3a2 + 2aа + b)x + (a3 + aa2 + ba + c) = 0.

Положим 3a + а = 0. Найдем отсюда a = - а/3 и подставим в выражения

 p = 3a2 + 2aа + b, q = a3 + аa2 + ba + c.

Тогда уравнение примет вид х3 + px + q = 0.

В нашей символике это уравнение соответствует уравнениям (1), (2), которые решал Тарталья.

Кардано узнал способ решения уравнений третьей степени, предложенный Тартальи, опубликовал его. Формула же стала носить название «формулы Кардано».

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки