Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

ахm – xm+n = b

имеющем по условию два корня, он определил коэффициенты, при которых корни уравнения имели бы заданные значения.

Пусть эти корни у и z. Тогда

a =, b =

Ту же задачу он решил относительно уравнения

xm+n + axm = b, где m + n – число четное, m – нечетное.

Чрезвычайно важно то, что Виет распространил известные ранее частные преобразования на все алгебраические уравнения. Подстановку х = у + k, применявшуюся Кардано для исключения из кубического уравнения члена второй степени, он применил к уравнениям любой степени. Также известную Кардано обратную подстановку х = k/y Виет употреблял, чтобы освободиться в некоторых случаях от отрицательных коэффициентов и иррациональностей. Например, уравнение х4 – 8х = подстановкой х =  он преобразовал к виду y4 + 8у3 = 80. Подстановкой х = y Виет преобразовывал уравнение n-й степени так, что коэффициент при члене (n -1)-й степени (a) становился равным b, в то время как старший коэффициент оставался равным единице. Подстановку х = ky он применял, чтобы избавиться от дробных коэффициентов.

Особый интерес представляет исследование Виета по составлению уравнений из линейных множителей и по установлению связей между корнями уравнения и его коэффициентами. Первоначальные сведения и по тому, и по другому вопросу были у Кардано.

Кардано в ту пору, когда еще не знал метода дель Ферро и Тартальи, решал некоторые уравнения третьей степени разложением на множители. В уравнении

2х3 + 4x2 + 25 = l6x + 55

с этой целью он прибавлял к обеим частям 2x2 + 10x + 5. Затем преобразовывал его к виду (2х + 6)(х2 + 5) = (х + 10)(2х + 6), сокращал на 2х + 6 и получал квадратное уравнение.

Кардано же при нахождении положительного корня уравнения х3 + b = ах складывал его почленно с уравнением у3 = ay + b, получал из них квадратное уравнение делением на х минус известный отрицательный корень х – (–у). Такое преобразование позволило Кардано установить, что коэффициент при члене второй степени в правой части кубического уравнения равен сумме его корней. Это был первый шаг к установлению зависимости между корнями и коэффициентами алгебраического уравнения.

Виет составил полные уравнения с заданными положительными корнями вплоть до пятой степени и показал, как образуются коэффициенты при xn-1, xn-2, xn-3, ... Он установил, что эти коэффициенты при условии, что старший коэффициент равен 1 или –1 (свободный член в правой части должен был стоять со знаком +), представляют собой взятые с чередующимися знаками суммы: самих корней, парных произведений их, произведений корней, взятых по три, и т. д. Работа, в которой Виет подробно рассмотрел это утверждение, до нас не дошла. Неизвестно, как он поступал в том случае, когда уравнение имеет и отрицательные корни. Но, скорее всего, это не представляло для Виета особых трудностей: достаточно было сделать в уравнении замену х = –у и можно оперировать с положительными корнями нового уравнения. Такие примеры в его работах встречались. Если уравнение х3 + q = рх имеет два положительных корня х1 и х2, то уравнение y3 = ру + q – один положительный корень у1 = –х3 причем у1 = х1 + х2 (это знал Кардано), x12 + x22 + x1x2 = p, x1x2(x1 + x2) = q.

Как видим, в исследованиях Виета встречались начала теории симметрических функций и разложения многочленов на линейные множители, что вскоре привело к открытию основной теоремы алгебры о числе корней уравнения произвольной степени. Эти исследования Виета продолжили математики следующего поколения Т. Гарриот (1560— 1621), А.Жирар (1595-1632), Р. Декарт (1596-1650).

2.3 Символика Декарта и развитие алгебры.

В сочинении «Исчисление г. Декарта» неизвестный автор изложил арифметические основы математики Декарта. Они писал: «Эта новая арифметика состоит из букв a, b, c и т.д., а также из цифр 1, 2, 3 и т.д. Если цифры стоят перед буквами, например, 2а, 3b, 1/4с, то это означает, что величина а берется двойной, величина b – тройной, а от величины с берется четверть. Но если они находятся позади букв, например, а3, b4, c5, то это означает, что величина а умножается сама на себя три раза, величина b – четыре раза, а величина с – пять раз». «Сложение производится с помощью такого знака +. Так, чтобы сложить а и b, я пишу а + b. Вычитание производится с помощью такого знака –. Так, чтобы вычесть а из b, я пишу b – a и т. д. Если в вычитаемом выражении есть несколько частей, то у них в нем изменяются лишь знаки. Так, если из d требуется вычесть а – b + с, то останется d – а + b – –с. Точно так же при вычитании а2 – b2 из с2 – d2 останется с2 – d2 – а2 + b2. Но если имеются присоединенные цифры и члены одинакового вида, то их следует подписывать друг под другом и производить их сложение и вычитание как в обыкновенной арифметике... Если требуется умножить одну букву на другую, то их следует лишь соединить вместе, но если имеются присоединенные, числа, то они следуют законам обыкновенной арифметики. Что касается знаков, то известно, что + на + дает в произведении + и что –, умноженный на –, также дает в произведении +. Но + на – или же –, умноженный на +, дает в произведении –».

Точно так же определялись действие деления, операции с дробями «по правилам обыкновенной арифметики». Вот рассуждение о корне: «Когда корень извлечь из квадрата нельзя, его квадрат помещают под связку , чтобы отметить, что его следует рассматривать как корень, и тогда его корень называют иррациональной величиной».

Из всего этого видно, как далеко зашла формализация алгебраических действий по сравнению с тем, что было у древних греков и у предшественников Декарта; видно также, что надобности в геометрической интерпретации алгебры уже нет.

Формализации алгебры (и всей математики) чрезвычайно способствовало то, что Декарт усовершенствовал буквенную символику. Он обозначал известные величины буквами а, b, с, . . ., неизвестные («неопределенные») – буквами x, y, z, .... Он ввел обозначения степеней: a2, a3 , х3 , . . . Правда, квадраты величин он выражал и с помощью символов аа, хх. Обозначение корня несколько отличается от современного. Так, выражение 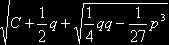означает один из кубических корней, входящих в формулу Кардано.

Все буквы в формулах Декарта считались положительными величинами; для обозначения отрицательных величин ставился знак минус; если знак коэффициента произволен, перед ним ставилось многоточие. Знак равенства имел необычный вид . Вот как, например, выглядело уравнение с произвольными коэффициентами:

+x4…px3…qx… 0.

И еще один символ применял Декарт: он ставил звездочки, чтобы показать отсутствующие члены уравнения, например:

 x5*** – b  0.

Другие математики того времени тоже пользовались символикой, близкой к разработанной Декартом, а древние греки излагали свои мысли вообще без символики. Ферма построил аналитическую геометрию, располагая запасом употребляемых до него алгебраических средств. «...все это может побудить нас недооценить те успехи, которые поставлены здесь во главу всей математической деятельности Декарта. Значение этих успехов становится, однако, понятным, если мы примем во внимание, как часто мы должны были для изложения идей более ранних авторов прибегать к пользованию алгебраической формой Декарта; без нее мы вряд ли смогли бы это сделать сколь-нибудь сжато и наглядно. Мы смогли воспользоваться этой алгебраической формой, с одной стороны, потому что декартова трактовка алгебры благодаря своим преимуществам получила ныне широкое распространение, и знакомство с ней происходит уже в школе. С другой стороны, она уже сама по себе в большой мере расчистила путь многому, что раньше могло быть изложено лишь весьма громоздким образом и было поэтому доступно лишь очень способным математикам» (Цейтен Г. Г, История математики в XVI и XVII веках, с. 202)

Иными словами, разработка и введение алгебраической символики сделали математику более демократичной.

Уравнения, по утверждению Декарта, представляют собой равные друг другу суммы известных и неизвестных членов или же, если рассматривать эти суммы вместе, равны «ничему» (нулю). Декарт указал, что «уравнения часто удобно рассматривать именно последним образом», т. е. в виде Р (х) = 0. Для теоретических построений Декарта такая запись уравнений играла важную роль.

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки