Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата



Вероятностное пространство

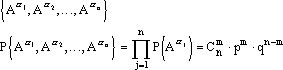
В этом примере s-алгеброй является множество всех подмножеств пространства элементарных событий. Введенную нами случайную величину x по определению можно задать:

- верхняя строчка - это совокупность возможных числовых значений, которые может принимать случайная величина;

- нижняя строчка - вероятность наступления этих числовых значений.

Практически во всех задачах естествознания отсутствует промежуточный этап: испытание, W - пространство всех возможных исходов испытания, - числовая скалярная функция, элементы которой wÌW.

На самом деле структура:

- испытание;

- исход испытания;

- число на числовой оси.

Вероятностные характеристики дискретных случайных величин.

Математическим ожиданием случайной величины X называется число вида

xi - все возможные различные конкретные исходы испытания;

pi - вероятности их наступления.

Математическое ожидание является как бы аналогом центра масс точечной механической системы:

Как центр масс:

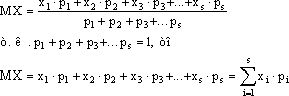
Смысл характеристики мат.ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной.

Свойства математического ожидания

1. MC=C

2. MCX=CMX

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки