Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

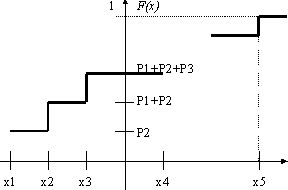
Производная функция

Характеристической функцией случайной величины X называется функция действительного аргумента вида

Производящей функцией называется скалярная функция вида:

Свойства производящей функции

1.

2.

 

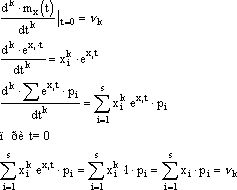
3. Разложение производящей функции в ряд Маклорена имеет вид

Формула Тейлора имеет вид

при to=0 она носит название формулы Маклорена

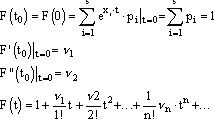
Пример:

Рассмотрим случайную величину, распределенную по биноминальному закону распределения:

Найдем производящую функцию:

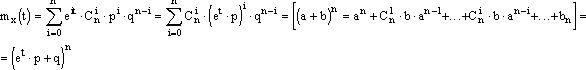
Найти DX и MX

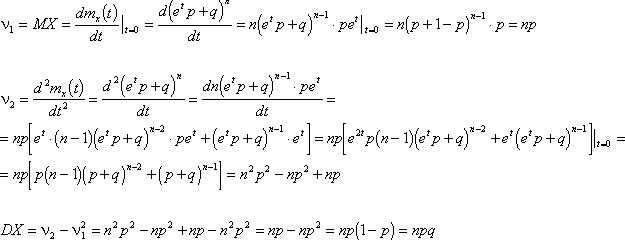
Первая модель распределения Пуассона

Проведена неограниченно большая серия испытаний, в результате каждого испытания случайным образом появляется точка на числовой оси. Случайное распределение точек на числовой оси удовлетворяет следующим трем свойствам.

1. Стационарность. Вероятность того, что на отрезок данной длины попадает данное количество точек определяется только длиной этого отрезка и не зависит от расположения этого отрезка на числовой оси.

2. Ординарность. Вероятность того, что на достаточно малый отрезок длины Dx попадает одна точка, является бесконечно малой Dx порядка. Вероятность того, что на этот отрезок попадает более, чем одна точка, является бесконечно малой более высокого порядка, чем Dx.

3. Свойство без последействия. Вероятность того, что на данный отрезок попало определенное количество точек не зависит от того, сколько точек в результате проведенной бесконечно серии испытаний попало на отрезок, не пересекающийся с данным.

Найти вероятность того, что на данный отрезок длина l попадает m точек.

Обозначим через xl - случайная величина, равная численности точек, выпавших на отрезок длины l.

На числовой оси рассмотрим отрезок длины 1 и обозначим:

MX1=l

Математическое ожидание числа точек, попавших на отрезок длины 1. По свойству стационарности l одинаково для всех отрезков.

MX1=ll - доказать

Пусть l - целое число. Разобьем отрезок длины l на l отрезков единой длины. Тогда количество точек, попавших на отрезок длины l будет равно числу точек, попавших на каждый из непересекающихся отрезков длины 1 (тут использовалось свойство беспоследействия).

Используя формулу

имеем

MX1=ll

Математическое ожидание числа точек, попавшие на отрезок длины l равно мат. ожиданий точек, попавших на непересекающиеся отрезки. Пусть l - не целое число. Выделяем целую часть. Тогда

На числовой оси рассмотрим отрезок длины l, разобьем его на n отрезков данной длины

такой, что позволит использовать свойство ординарности. Тогда с определенной погрешностью, которая тем меньше, чем больше n можно считать

т.е. на отрезок длины Dx попадает не более, чем одна точка, тогда

Для достаточного малого отрезка длины lDx вероятность попадания в него одной точки Dx, а вероятность того, что ничего не произойдет 1- lDx.

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки