Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата



т.к.

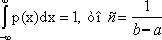
Экспоненциальное распределение.

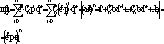
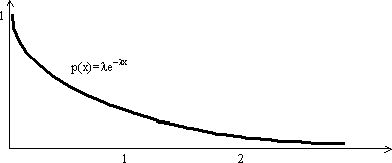
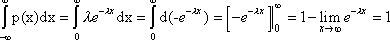
Непрерывная случайная величина является математической абстракцией и в чистом виде на практике не встречается, хотя бы потому, что теоретически не может существовать измерительное устройство, вычисляющее это величину. Следовательно, всегда исследователь имеет дело со случайными дискретными величинами. На практике отрезок [a, b] разбивают на отрезки одинаковой длинны, длину устремляют к нулю. При этом x принадлежит отрезку. Вероятность того, что отрезок содержит x равна . При  ситуация эквивалентна следующему: имеется бесконечное множество лотерейных билетов, один ваш. Ясно, что в конечной серии розыгрышей вы никогда не выиграете. Независимо от этого велико удобство работы с непрерывными величинами. Оно заключается в том, что вероятностные свойства задаются одной из двух функций - плотностью распределения либо плотностью вероятности.

Вероятностные характеристики непрерывных случайных величин.

Пусть имеется случайная величина, являющаяся функцией от непрерывной случайной величины X.

Y=x(x)

Математическим ожиданием непрерывной случайной величены является число:

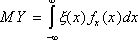, - плотность вероятности случайной величины.

Обоснование этой формулы.

Аппроксимируем непрерывную случайную величину Y случайной величены Y*, которая является дискретной. Пусть числовая ось - пространство элементарных событий случайной величены X, разобьем всю числовую ось на отрезки достаточно малой длины.

2n отрезков.

Если в результате испытания случайная величена X попала в отрезок с начальной вершиной xi, то случайная величена X* приняла значение x(xi) с точностью до бесконечно малой Dx - длины i-го отрезка. Вероятность того, что Y* примет значение x(xi) с точностью до бесконечно малой более высокого порядка, чем Dx, тем более точно Y* аппроксимирует Y.

Вероятность наступления x(xi) для Y* равна

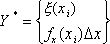
, при эта сумма переходит в .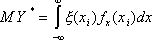

Тогда .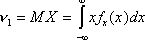

Самим показать, что все свойства мат. ожидания для дискретной случайной величены сохраняются для непрерывной случайной величены.

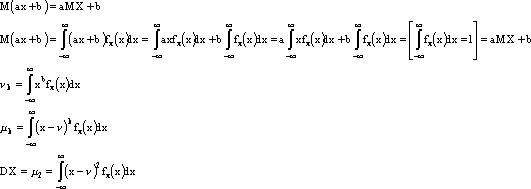
Доказать, что

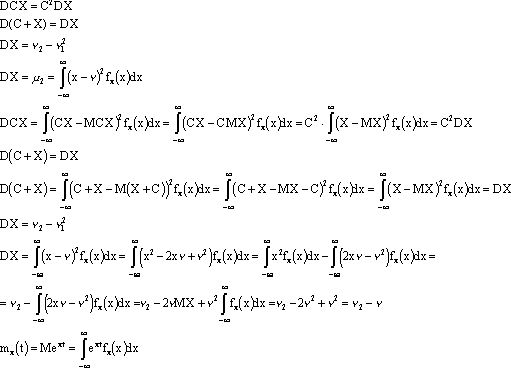
Доказать самим, что свойство 1 и 2 для производящей функции в дискретном случае справедливы и для непрерывного.

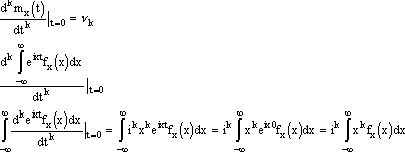
Распределение Гаусса - нормальное

Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности

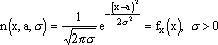
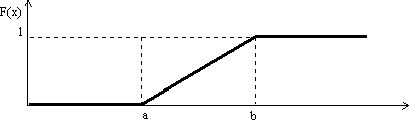
Из определения

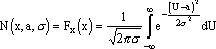
функция распределения

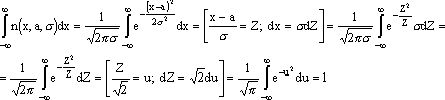
Найдем выражение для производящей функции нормального распределения

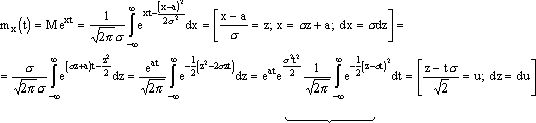
                                    =1 (интеграл Эйлера)

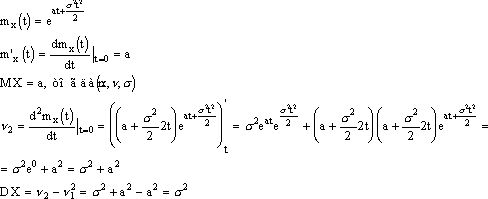
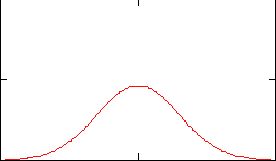
Изобразим примерный вид плотности

n(x,n,s)

v

	z

Рассмотрим центрированную нормальную величину, т.е. MX=0

У центральной нормированной величины все нечетные начальные моменты равны 0

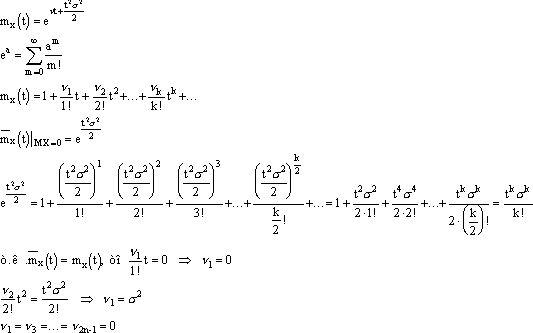
Функция Лапласа

Функцией Лапласа называется функция вида

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки