Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

такой, что позволит использовать свойство ординарности. Тогда с определенной погрешностью, которая тем меньше, чем больше n можно считать

т.е. на отрезок длины x попадает не более, чем одна точка, тогда

Для достаточного малого отрезка длины lx вероятность попадания в него одной точки x, а вероятность того, что ничего не произойдет 1- x.

В сделанных предположениях m точек попадает на отрезок длины l только в одном случае, когда в m отрезках попадает по одной точке. Тогда на основании 3-го свойства искомая вероятность равна

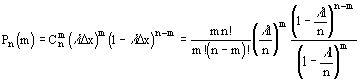
Точную вероятность получим путем предельного перехода при числе разделений отрезка

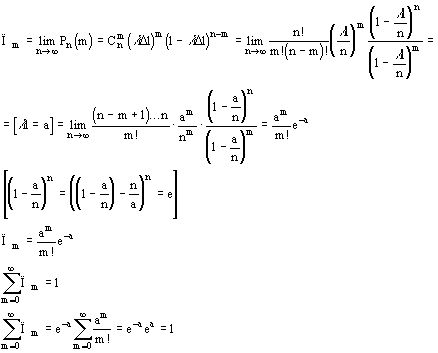
Тут мы разложили в ряд Маклорена.

Найдем производящую функцию распределения Пуассона

Найти MX и DX

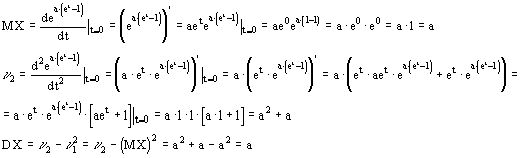
Вторая модель распределения Пуассона

Рассматривается обычная схема биноминального распределения, в котором n - велико, а p - достаточно мало. Тогда точная формула для вероятности появления события A в m испытаниях имеет вид

Эта формула при больших n вычисляется сложно. Такую вероятность заменяют приближенной

Для найденного a построим гипотетический ряд вероятностей

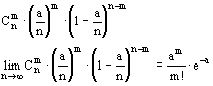
Предполагается, что для достаточно больших n и малых p искомая вероятность

является членом построенного гипотетического ряда вероятностей, а во вторых находится в малой окрестности предельного значения этого ряда. И, следовательно, это значение можно взять в качестве допустимой хорошей аппроксимации значений искомой вероятности.

Непрерывные случайные величины.

Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. В этом случае введенная ранее функция распределения имеет вид: .

Пусть функция распределения является непрерывной. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число.

P(X=a).

Рассмотрим неравенство:

Доказать самим.

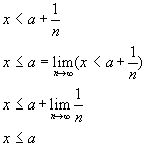
Следовательно:

Мы впервые столкнулись с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0 . В инженерном толковании это означает: в данной конечной серии испытаний данное событие никогда не произойдет.

Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

P(a£ X<b)=P(a£ X£ b)=F(b)-F(a)

Если от сложного события вычесть конечное либо счетное множество, вероятность наступления нового события останется неизменной.

Функция f(x) - числовая скалярная функция действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:

Свойства плотности вероятности.

Плотность вероятности является неотрицательной функцией.

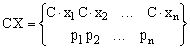
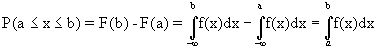
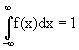
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0.

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки

   

Категории:

• Математика