Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

.

            Положив 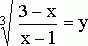, после подстановки получим уравнение

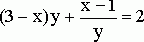
или эквивалентное ему уравнение

,

которое можно рассматривать как квадратное уравнение относительно . Решая это уравнение, получим

,           .

Следовательно, множество решений исходного иррационального уравнения представляет собой объединение множеств решений следующих двух уравнений:

, .

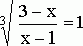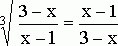            Возведя обе части каждого из этих уравнений в куб, получим два рациональных алгебраических уравнения:

,                  .

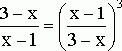            Решая эти уравнения, находим, что данное иррациональное уравнение имеет единственный корень .

            В заключение заметим, что при решении иррациональных уравнений не следует начинать решение уравнение с возведения обеих частей уравнений в натуральную степень, пытаясь свести решение иррационального уравнения к решению рационального алгебраического уравнения. Сначала необходимо посмотреть, нельзя ли сделать какое-нибудь тождественное преобразование уравнения, которое может существенно упростить его решение.

            П р и м е р 3. Решить уравнение

                                                 .                                                 (20)

Множество допустимых значений данного уравнения: . Сделаем следующие преобразования данного уравнения:

.

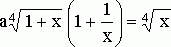
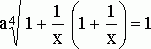Далее, записывая уравнение в виде

,

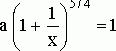получим:

            при  уравнение решений иметь не будет;

            при  уравнение может быть записано в виде

.

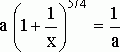            При  данное уравнение решений не имеет, так как при любом , принадлежащем множеству допустимых значений уравнения, выражение, стоящее в левой части уравнения, положительно.

            При  уравнение имеет решение

Рекомендуем скачать другие рефераты по теме: урок реферат, реферат данные.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки