Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

.

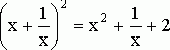Поэтому величина  удовлетворяет квадратному уравнению

,

решив которое можно найти  из уравнения .

            При решении возвратных уравнений более высоких степеней обычно используют тот факт, что выражение  при любом  можно представить как многочлен степени  от .

Рациональные алгебраические уравнения

Рациональным алгебраическим уравнением называется уравнение вида

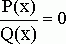                                                                  ,                                                                  (17)

где  и  - многочлены. Далее для определенности будем полагать, что  - многочлен m-й степени, а  - многочлен n-й степени.

            Множество допустимых значений рационального алгебраического уравнения (17)

задается условием , т. е. , , ...,  где , , ...,  - корни многочлена .

            Метод решения уравнения (17) заключается в следующем. Решаем уравнение

,

корни которого обозначим через

.

Сравниваем множества корней многочленов  и . Если никакой корень многочлена  не является корнем многочлена , то все корни многочлена  являются корнями уравнения (17). Если какой-нибудь корень многочлена  является корнем многочлена, то необходимо сравнить из кратности: если кратность корня многочлена  больше кратности корня многочлена , то этот корень является корнем (17) с кратностью, равной разности кратностей корней делимого и делителя; в противном случае корень многочлена  не является корнем рационального уравнения (17).

            П р и м е р. Найдем действительные корни уравнения

,

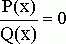где , .

Многочлен  имеет два действительных корня (оба простые):

, .

Многочлен  имеет один простой корень . Следовательно, уравнение имеет один действительный корень .

            Решая то же самое уравнение в множестве комплексных чисел, получим, что уравнение 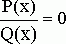 имеет, кроме указанного действительного корня, два комплексно сопряженных корня:

, .

Иррациональные уравнения

Рекомендуем скачать другие рефераты по теме: урок реферат, реферат данные.



Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки