Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Удовлетворяя (10) краевым условиям (7) и (8), имеем:

                 (11)

Теперь построим общее решение для уравнения (8). Для этого в (8) введем новую переменную  Тогда оно примет вид:

        (12)

Уравнение (12) является гипергеометрическим уравнением [9, с. 69], и поскольку a не является целым числом, то общее решение уравнения (8) определяется по формуле

    (13)

Функция (13) удовлетворяет первому граничному условию из (9). Удовлетворим (13) второму краевому условию из (9).

        (14)

На основании равенств [10, с. 112]

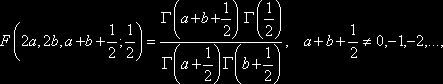
имеем уравнение для нахождения неизвестного :

     (15)

В силу известных формул

имеем:

 где

Тогда с учетом того, что и  равенство (15) примет вид:

    (16)

Таким образом, в области D+ найдены частные решения уравнения (1), удовлетворяющие краевому условию  (3):

(17)

3. Построение частных решений в области гиперболичности. В уравнение (1) в области D- сделаем замену переменных  Тогда в координатах  уравнение (1) примет вид:

Рекомендуем скачать другие рефераты по теме: шпоры по праву, 2 класс изложение.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки