Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Разделив переменные  получим:

          (18)

             (19)

        (20)

           (21)

Решением уравнения (18) , удовлетворяющего условиям (19), является функция

        (22)

Уравнение (20) так же, как и уравнение (12), является гипергеометрическим уравнением с аргументом . Переходя к аргументу , построим его общее решение:

   (23)

Если  то функция (23) удовлетворяет граничным условиям (21). Тогда решением уравнения (20), удовлетворяющего условиям (21), будет:

Таким образом, в области D- найдены частные решения уравнения (1), удовлетворяющие граничному условию (4):

         (24)

4. Построение собственных функций задачи Tl. Для нахождения собственных значений и собственных функций задачи Tl  , построенную систему функций (17) и (24) удовлетворим условиям склеивания (2) и (5).

Из (17) и (24) вычислим:

Приравнивая функции

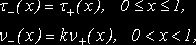
получим систему

из которой находим коэффициенты  и :

   (25)

Рекомендуем скачать другие рефераты по теме: шпоры по праву, 2 класс изложение.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки