Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

где L4, L3, L2 - дифференциальные операторы в частных производных 4-го, 3-го и 2-го порядков:

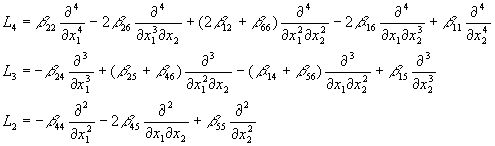
Уравнения (18) представляют собой систему 2-х дифференциальных уравнений в частных производных. Уравнения - линейные, неоднородные, с постоянными коэффициентами.

Общее решение системы (18) для функций напряжения можно представить в виде:

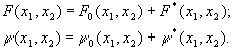
F0 и y 0 - общее решение соответствующей однородной системы:

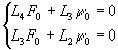(19)

F* и y * - частные решения неоднородной системы уравнений (18). Частные решения зависят от правых частей уравнений и если эти правые части несложны, то и частные решения обычно описать нетрудно.

Чтобы получить общее решение однородной системы (19) исключим из нее y 0:

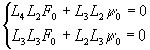(20)

В силу симметрии L их можно менять местами:

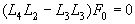(21)

Таким образом, мы получили линейное дифференциальное уравнение 6-го порядка для функции F. Аналогично находим уравнение для y :

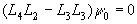(22)

Оказалось, что F0 и y 0 должны удовлетворять одинаковым условиям. Оператор 6-го порядка можно разложить на 6-ть линейных операторов 1-ого порядка Dk и уравнение (21) представить в виде:

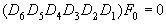(23)

Из теории диф. уравнений и условия что функция F0 зависит только от x1 и x2 для Dk имеем:

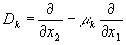(24)

где 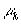- это корни алгебраического (характеристического) уравнения шестой степени, соответствующего дифференциальному уравнению (21).

Интегрирование линейного уравнения 6-го порядка можно свести к последовательному интегрированию шести уравнений первого порядка. В результате получим следующие общие выражения:

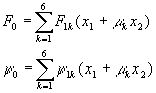
Если среди корней характеристического уравнения есть кратные, задача упрощается, однако решение системы (19) может быть найдено в любом случае исходя из следующих рассуждений.

Любые 6 вещественных чисел можно принять в качестве значений независимых компонент тензора напряжений в данной точке упругого анизотропного тела. Удельная потенциальная энергия деформации есть величина положительная при любых вещественных и не равных нулю значениях компонент тензора напряжений в данной точке. Исходя из этих предположений можно доказать теорему, согласно которой алгебраическое характеристическое уравнение системы (21), не имеет вещественных корней. Поэтому можно утверждать, что числа 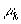в общем решении системы (19), а также в условиях связи всегда комплексные или чисто мнимые.

Наряду с комплексными параметрами вводят и систему комплексных переменных:

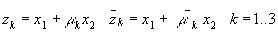
Рекомендуем скачать другие рефераты по теме: конспект урока 9 класс, сочинение 6 класс.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки