Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Введение комплексных переменных позволяет использовать при аналитическом решении рассматриваемой задачи об упругом равновесии анизотропного тела математический аппарат и методы функций комплексных переменных. Эти методы, применительно к данной задаче являются очень эффективными и позволяют получить аналитическое решение многих плоских задач теории упругости анизотропного тела.

2. Прикладная часть 2.1 Физическая постановка задачи.

Рассмотрим бесконечную пластинку из ортотропного материала с эллиптическим отверстием в центре. Направление главных осей эллипса совпадает с главными осями упругости материала, усилия приложены на бесконечности вдоль главных осей.

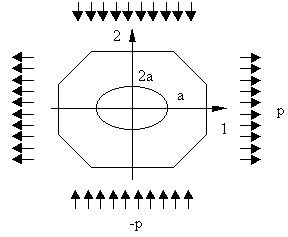
Введем следующие обозначения 2a, 2b - главные оси эллипса, с=a/b, р - усилие на единицу площади. В нашем случае отношение полуосей эллипса с=1/2. Вдоль оси 1 на бесконечности приложено растягивающее усилии р, а вдоль оси 2 - сжимающее -р. Наша задача найти напряжения на краю отверстия и построить их эпюру.

2.2 Упругие свойства материала.

Пластинка сделана из стеклопластика C-II-32-50 со следующими характеристиками:

Е1=13,0 ГПа;

Е2=19,8 ГПа;

Е3=7,8 ГПа;

G12=4,05 ГПа;

G13=6,4 ГПа;

G23=3,2 ГПа;

n 13=0.25;

n 32=0.14;

n 12=0.176;

n 23=0.06.

2.3 Математическая постановка задачи.

Уравнения равновесия применительно к нашей задаче, когда напряжения зависят только от двух координат и fi=0, запишутся так:

Граничные условия будут иметь следующий вид:

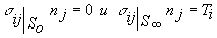
или в развернутом виде применительно к нашей задаче:

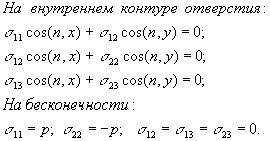
где n - нормаль к контуру отверстия.

2.4 Аналитическое решение.

Решая данную задачу по методу изложенному в первой части с учетом того, что материал у нас ортотропный выясняем что характеристическое уравнение для определения коэффициентов 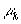распадается на уравнения 4 и 2 степени:

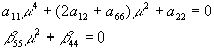
Отсюда немедленно вытекают следующие соотношения:

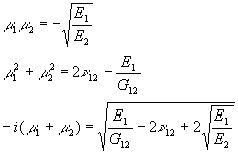
Рекомендуем скачать другие рефераты по теме: конспект урока 9 класс, сочинение 6 класс.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки