Рефераты | Рефераты по эргономике | О некоторой общей схеме формирования критериев оптимальности в играх с природой О некоторой общей схеме формирования критериев оптимальности в играх с природой Категория реферата: Рефераты по эргономике Теги реферата: зимнее сочинение, реферат на тему образование Добавил(а) на сайт: Karsakov. Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата	r-a
10.4	+	+	+	qr-(1-q)a	(1-q)r-qa

Оптимальной по критерию является стратегия Ai0, для которой

.

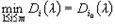Данный критерий превращается в минимаксный критерий при  = 0, в миниминный критерий при  = 1, в критерии Гурвица относительно рисков при 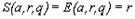(критерий 10.1).

Утверждение 4. При одном и том же коэффициенте оптимизма 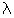максиминно-максимаксные критерии 9.3 и 9.4 эквиваленты соответственно минимаксно-миниминным критериям 10.3 и 10.4.

Доказательство. Для критериев 10.3 и 9.3 имеем:

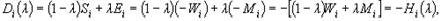
откуда

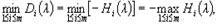
т.е. показатель неоптимальности Di( ) будет минимальным для того значения i, для которого показатель оптимальности Hi( ) будет максимален. Таким образом, эквиваленция 9.3  10.3 доказана.

Эквиваленция 9.4  10.4 доказывается аналогично. n

ПРИМЕР. Рассмотрим игру с природой, в которой игрок А имеет возможность применить одну из четырех стратегий А1, А2, А3, А4, а природа П может находиться в одном из трех состояний П1, П2, П3 с вероятностями соответственно q1 = 0,7; q2 = 0,1; q3 = 0,2. Известны выигрыши (aij) игрока А. Найдем оптимальные стратегии по рассмотренным выше критериям.

Выпишем таблицы показателей игры и в дополнительных столбцах – показатели оптимальности и неоптимальности для соответствующих критериев. При этом на основании утверждений 1-4 из эквивалентных критериев будем рассматривать только один.

Главная | Партнеры | Лучшие рефераты

Обратная связь

Рефераты | Рефераты по эргономике | О некоторой общей схеме формирования критериев оптимальности в играх с природой | страница реферата 16 | Большая Энциклопедия Рефератов от А до Я    Все рефераты, курсовые, дипломы, шпаргалки, сочинения, изложения, решебники, конспекты являются общедоступными    Копирование и размещение в интернете разрешается только при наличии активной индексируемой ссылки на Ahaha.ru

© 2006-2020 «Ahaha.ru»