Рефераты | Рефераты по эргономике | О некоторой общей схеме формирования критериев оптимальности в играх с природой
О некоторой общей схеме формирования критериев оптимальности в играх с природойКатегория реферата: Рефераты по эргономике Теги реферата: зимнее сочинение, реферат на тему образование Добавил(а) на сайт: Karsakov. Предыдущая страница реферата | 8 9 10 11 12 13 14 15 16 17 18 | Следующая страница реферата |
|
|
|
Из
этой таблицы очевидно, что поскольку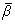 
для данной
матрицы выигрышей (aij) есть величина постоянная, то показатель неоптимальности
Ki в каждой клетке обращается в минимум при том же значении i, при котором
показатель оптимальности Li обращается в максимум. Следовательно, имеем
следующие эквиваленции критериев:
7.1 8.1, 7.1 8.2, 7.2 8.1, 7.2 8.2, из которыx следует требуемая экиваленция (13).
Отметим, что эквиваленция 7.1 8.1 – известный факт (доказанный, например, в [1], с. 502).
Из эквиваленции (13) можно сделать вывод о том, что из критериев 7.1, 7.2, 8.1, 8.2 достаточно применить один, причем с более простой функцией игры.
Максиминно-максимаксные критерии.
Такие
критерии представляют собой комбинации максиминного и максимаксного критериев.
В качестве показателя оптимальности стратегии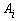 
берется
величина
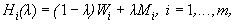
где
[0,1]– коэффициент оптимизма, а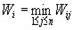 
и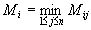 
– показатели оптимальности стратегии Ai
соответственно в максиминном и максимаксном критериях (см. п. 3 и п. 5). При
этом функции игры в этих двух критериях целесообразно использовать
соответствующие друг другу. Это соответствие показано в табл. 3.
Таблица 3
|
Критерии |
Выигрыши a |
Риски r |
Вероятности состояний природы q |
W (a, r, q) |
M (a, r, q) |
|||
|
9.1 |
+ |
a Рекомендуем скачать другие рефераты по теме: цель реферата, ответы по контрольной. Предыдущая страница реферата | 8 9 10 11 12 13 14 15 16 17 18 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
