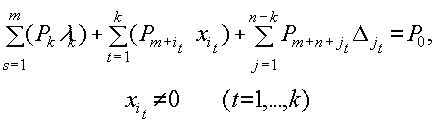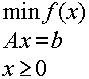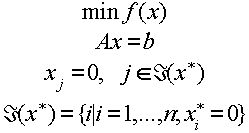Формирование инвестиционного портфеля
Категория реферата: Рефераты по информатике, программированию
Теги реферата: bestreferat ru, реферат катастрофы
Добавил(а) на сайт: Альбертина.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Базис UÁ 1,Á 2 назовем оптимальным, если его базисные переменные удовлетворяют условиям Куна-Таккера (3.2.3).
Базис называется невырожденным, если все его базисные переменные, соответствующие компонентам вектора x отличны от нуля, т.е.
|
|
(3.3.4) |
Задачу (3.1.2) будем называть невырожденной, если все ее базисы невырождены. В противном случае назовем задачу вырожденной.
3.4. Метод субоптимизации на многообразиях. Выпуклый случай.
Для решения задачи (3.1.2) предлагается использовать метод
субоптимизации на многообразиях. Вначале рассмотрим основные идеи, приводящие к методу субоптимизации в случае задачи выпуклого программирования общего вида.
Рассмотрим задачу выпуклого программирования с линейными ограничениями, состоящую в минимизации выпуклой функции f(x) на множестве L, задаваемом ограничениями типа равенств.
|
|
(3.4.1) |
Предположим, что задача имеет единственное решение, т.е минимум целевой функции достигается в единственной оптимальной точке x*. В этом случае задаче (3.4.1) эквивалентна задача:
|
|
(3.4.2) |
Эквивалентность этих двух задач является следствием единственности решения. Переход к задаче (3.4.2) называется выделением активных ограничений, т.е. вместо условия неотрицательности всех переменных, мы переходим к условию равенства нулю всех компонент, решения, индексы которых не принадлежат множеству Á (x*).
Предположим, что для задачи (3.4.2) нахождение оптимального решения существенно проще, чем для исходной задачи (3.4.1). В этом случае, перебирая каким-либо образом всевозможные множества индексов Á k, являющиеся подмножествами полного набора индексов {1,..n}, и решая для каждого из них задачу (3.4.2), используя Á k вместо Á *, определить искомое множество индексов Á *.
Предположим также, что задача (3.4.2) обладает свойством
единственности, т.е система векторов {L1, .. Lm, ej (jÎ Á (x*)}- линейно независима. В случае нарушения свойства единственности задача поиска оптимального вектора задачи (3.4.2) усложняется, и в дальнейшем этот случай рассматриваться не будет.
Алгоритм перебора множеств индексов Á k основан на следующей лемме.
Основная лемма:
Пусть x* является оптимальной точкой задачи:
|
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |