
Абстрактная теория групп
Категория реферата: Рефераты по математике
Теги реферата: доклад на тему животные, сочинения по литературе
Добавил(а) на сайт: Rudov.
Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата
Всякая бесконечная циклическая группа изоморфна Z. Циклическая группа порядка n изоморфна Z / nZ .
Доказательство.
Пусть G = Z(g) - циклическая группа. По определению, отображение 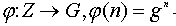 -
сюръективно. По свойству степеней
-
сюръективно. По свойству степеней 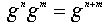 и потому j - гомоморфизм. По теореме о гомоморфизме
и потому j - гомоморфизм. По теореме о гомоморфизме
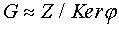 . H = Kerj
Ì Z. Если H - тривиальная подгруппа, то
. H = Kerj
Ì Z. Если H - тривиальная подгруппа, то 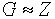 .
Если H нетривиальна, то она содержит положительные числа. Пусть n - наименьшее
положительное число входящее в H. Тогда nZÌ
H. Предположим, что в H есть и другие элементы то есть целые числа не делящееся
на n нацело и k одно из них. Разделим k на n с остатком: k = qn +r , где 0 <
r < n. Тогда r = k - qn Î H , что противоречит
выбору n. Следовательно, nZ = H и теорема доказана.
.
Если H нетривиальна, то она содержит положительные числа. Пусть n - наименьшее
положительное число входящее в H. Тогда nZÌ
H. Предположим, что в H есть и другие элементы то есть целые числа не делящееся
на n нацело и k одно из них. Разделим k на n с остатком: k = qn +r , где 0 <
r < n. Тогда r = k - qn Î H , что противоречит
выбору n. Следовательно, nZ = H и теорема доказана.
Отметим, что 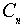 »
Z / nZ .
»
Z / nZ .
Замечание.
В процессе доказательства было установлено, что каждая подгруппа группы Z имеет вид nZ , где n = 0 ,1 , 2 ,...
Определение.
Порядком элемента 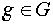 называется порядок соответствующей циклической подгруппы Z( g ) .
называется порядок соответствующей циклической подгруппы Z( g ) .
Таким образом, если порядок g бесконечен, то все степени 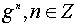 - различные элементы группы G. Если же этот порядок равен n, то элементы
- различные элементы группы G. Если же этот порядок равен n, то элементы 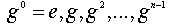 различны и исчерпывают все элементы из Z( g ), а
различны и исчерпывают все элементы из Z( g ), а 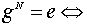 N кратно n . Из теоремы Лагранжа вытекает, что порядок элемента является делителем порядка группы. Отсюда следует, что для всякого элемента g конечной группы G порядка n имеет место равенство
N кратно n . Из теоремы Лагранжа вытекает, что порядок элемента является делителем порядка группы. Отсюда следует, что для всякого элемента g конечной группы G порядка n имеет место равенство 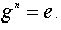 .
.
Следствие.
Если G - группа простого порядка p, то 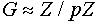 - циклическая группа.
- циклическая группа.
В самом деле, пусть 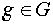 - любой элемент отличный от нейтрального. Тогда его порядок больше 1 и является делителем p, следовательно он равен p. Но в таком случае G = Z( g )»
- любой элемент отличный от нейтрального. Тогда его порядок больше 1 и является делителем p, следовательно он равен p. Но в таком случае G = Z( g )»
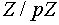 .
.
Теорема о подгруппах конечной циклической группы.
Пусть G - циклическая группа порядка n и m - некоторый делитель n. Существует и притом только одна подгруппа HÌ G порядка m. Эта подгруппа циклична.
Доказательство.
По предыдущей теореме G»
Z / nZ. Естественный гомоморфизм 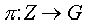 устанавливает взаимно однозначное соответствие между подгруппами HÌ
G и теми подгруппами KÌ
Z , которые содержат Kerp
= nZ . Но, как отмечалось выше, всякая подгруппа K группы Z имеет вид kZ Если kZÉ
nZ , то k - делитель n и p
(k) - образующая циклической группы H порядка m = n /k. Отсюда и следует утверждение теоремы.
устанавливает взаимно однозначное соответствие между подгруппами HÌ
G и теми подгруппами KÌ
Z , которые содержат Kerp
= nZ . Но, как отмечалось выше, всякая подгруппа K группы Z имеет вид kZ Если kZÉ
nZ , то k - делитель n и p
(k) - образующая циклической группы H порядка m = n /k. Отсюда и следует утверждение теоремы.
Верна и обратная теорема: если конечная группа G порядка n обладает тем свойством, что для всякого делителя m числа n существует и притом ровно одна подгруппа H порядка m, то G - циклическая группа.
Доказательство.
Будем говорить, что конечная группа G порядка N обладает свойством (Z), если для всякого делителя m числа N существует и притом только одна подгруппа HÌ G порядка m. Нам надо доказать, что всякая группа, обладающая свойством (Z) циклическая. Установим прежде всего некоторые свойства таких групп.
Лемма.
Если G обладает свойством (Z), то
Любая подгруппа G нормальна. Если x и y два элемента такой группы и их порядки взаимно просты, то xy = yx. Если H подгруппа порядка m такой группы G порядка N и числа m и N/m взаимно просты, то H обладает свойством (Z).Доказательство леммы.
1. Пусть HÌ G . Для любого 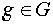 подгруппа
подгруппа 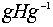 имеет тот же порядок,
что и H. По свойству (Z)
имеет тот же порядок,
что и H. По свойству (Z) 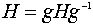 то
есть подгруппа H нормальна.
то
есть подгруппа H нормальна.
2. Пусть порядок x равен p, а порядок y равен q. По пункту 1) подгруппы Z(x)
и Z(y) нормальны. Значит, Z(x)y = yZ(x) и xZ(y) = Z(y)x и потому для некоторых
a и b 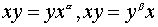 .
Следовательно,
.
Следовательно, 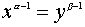 . Но, поскольку порядки
подгрупп Z(x) и Z(y) взаимно просты, то
. Но, поскольку порядки
подгрупп Z(x) и Z(y) взаимно просты, то 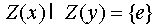 .
Следовательно,
.
Следовательно, 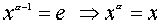 и потому xy = yx.
и потому xy = yx.
3. Используя свойство (Z) , выберем в G подгруппу K порядка N/m. По 1) эта
подгруппа нормальна, а поскольку порядки H и K взаимно просты, эти подгруппы
пересекаются лишь по нейтральному элементу. Кроме того по 2) элементы этих подгрупп
перестановочны между собой. Всевозможные произведения hk =kh, где hÎ
H, kÎ K попарно различны, так как 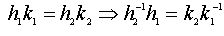 =e
поскольку это единственный общий элемент этих подгрупп. Количество таких произведений
равно m N/m =
=e
поскольку это единственный общий элемент этих подгрупп. Количество таких произведений
равно m N/m = 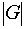 и, следовательно,
они исчерпывают все элементы G. Сюръективное отображение
и, следовательно,
они исчерпывают все элементы G. Сюръективное отображение 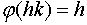 является гомоморфизмом
является гомоморфизмом 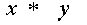 с ядром
K. Пусть теперь число s является делителем m. Выберем в G подгруппу S порядка
s. Поскольку s и N/m взаимно просты,
с ядром
K. Пусть теперь число s является делителем m. Выберем в G подгруппу S порядка
s. Поскольку s и N/m взаимно просты, 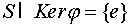 и потому
и потому 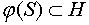 - подгруппа порядка s.
Если бы подгрупп порядка s в H было несколько, то поскольку все они были бы
и подгруппами G условие (Z) для G было бы нарушено. Тем самым мы проверили выполнение
условия (S) для подгруппы H.
- подгруппа порядка s.
Если бы подгрупп порядка s в H было несколько, то поскольку все они были бы
и подгруппами G условие (Z) для G было бы нарушено. Тем самым мы проверили выполнение
условия (S) для подгруппы H.
Рекомендуем скачать другие рефераты по теме: банк курсовых, шпори политология.
Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата