Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

там же при Z2 = Х, получаем, что существует класс Z такой, что

x1…xn (  Z  φ (x1,…,xn, Y1,…, Ym)).

Для остающегося случая xi  Yi теорема следует из (1) и

 XZ x v1…vm (  Z  x  X).

2. Предположим, что теорема доказана для любого k < s и что φ содержит s логических связок и кванторов.

(a) φ есть  ψ. По индуктивному предположению, существует класс W такой, что

x1…xn (  W  ψ (x1,…,xn, Y1,…, Ym)).

Теперь остается положить Z = .

(b) φ есть ψ θ. По индуктивному предположению, существуют классы Z1 и Z2 такие, что

x1…xn (  Z1  ψ (x1,…,xn, Y1,…, Ym)) и

x1…xn (  Z2  θ (x1,…,xn, Y1,…, Ym)).

Искомым классом Z в этом случае будет класс .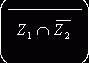

(c) φ есть x ψ. По индуктивному предположению, существует класс W такой, что

x1…xnx (  W  ψ (x1,…, xn, x, Y1,…, Ym)).

Применим сперва

 XZ x1 … xn (  Z y ( X)).

при X =  и получим класс Z1 такой, что

x1 … xn (  Z1x ψ (x1,…, xn, x, Y1,…, Ym)).

Теперь положим окончательно Z = , замечая, что x ψ эквивалентно

x ψ.

Примеры. 1. Пусть φ (X, Y1, Y2) есть формула uv (X =  & u   Y1 & v  Y2). Здесь кванторы связывают только переменные для множеств. Поэтому, в силу теоремы о существовании классов,  Z x (x  Z  uv (x =  & u  Y1 & v  Y2)), а на основании аксиомы объемности,  1Z x (x  Z  uv (x =  & u  Y1 & v  Y2)). Поэтому возможно следующее определение, вводящее новую функциональную букву :

Определение. x (x  Y1  Y2  uv (x =  & u  Y1 & v  Y2)). (Декартово произведение классов Y1 и Y2).

Определения.

X2 обозначает X  X (в частности, V2 обозначает класс всех упорядоченных пар).

…………………………………………………………………………………………………

Рекомендуем скачать другие рефераты по теме: конспекты статей, изложение с элементами сочинения.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки