Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

 P (0) = {0}.

 P ({0}) = {0, {0}}.

 P ({0, {0}}) = {0, {0}, {0, {0}}, {{0}}}.

Значительно более общим средством построения новых множеств является следующая аксиома выделения.

А к с и о м а S.

xY zu (u  z  u  x & u  Y).

Таким образом, для любого множества х и для любого класса Y существует множество, состоящее из элементов, общих для х и Y. Следовательно,  xY (M (x ∩ Y)), т. е. пересечение множества с классом есть множество.

Предложение 5.  xY (Y  x  M (Y)) (т. е. подкласс множества есть множество).

Доказательство.  x (Y  x Y ∩ x = Y) и  x (M (Y ∩ x)).

Так как всякая предикативная формула A(у) порождает соответствующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество.

Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений.

Определения

Un (X) означает xyz (  X &   X  y = z).

(X однозначен.)

Fnc (X) означает X  V2 & Un (X). (X есть функция.)

Y 1 X означает X ∩ (Y V). (Ограничение Х областью Y.)

Un1 (X) означает Un (X) & Un (). (X взаимно однозначен.)

X‘Y

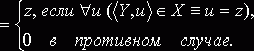
Если существует единственное z такое, что   X, то z = X‘y; в противном случае X‘y = 0. Если Х есть функция, а у — множество из области определения X, то X‘y есть значение этой функции, примененной к у (В дальнейшем будем по мере необходимости вводить новые функциональные буквы и предметные константы, как только будет ясно, что соответствующее определение может быть обосновано теоремой о единственности. В настоящем случае происходит введение некоторой новой функциональной буквы h с сокращенным обозначением Х‘Y вместо h (X, Y)).

X‘‘Y = R(Y 1 X). (Если Х есть функция, то X‘‘Y есть область значений класса X, ограниченного областью Y.)

А к с и о м а R. (Аксиома замещения.)

x (Un (X)  yu (u  y  v ( X & v  X))).

Аксиома замещения утверждает, что если класс Х однозначен, то класс вторых компонент тех пар из X, первые компоненты которых принадлежать, является множеством (эквивалентное утверждение: M(R (x 1X))) Из этой аксиомы следует, что если Х есть функция, то область значений результата ограничения Х посредством всякой области, являющейся множеством, также есть множество.

Следующая аксиома обеспечивает существование бесконечных множеств.

А к с и о м а I. (Аксиома бесконечности.)

Рекомендуем скачать другие рефераты по теме: конспекты статей, изложение с элементами сочинения.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки