Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Доказательство. Проверим инвариантность L. Для любых a, b С имеем

Р1 (aх + bР2х) = aх + λbх = (a + λb) х L,

Р2 (aх + bР2х) = aР2х + bР2х = (a + b) Р2 х L

dimL = 2, так как Нi,j = {0} (для всех i, j= 0,1).

Действительно, если aх + bР2х = 0, где, например, а ≠ 0, то х =  Р2х, значит = 0 или 1 и х Н1,1; тогда Н1,1≠{0}.

Итак, получаем предложение.

Теорема 1.2. Если dimН = n, n>2, то нет неприводимых *-пред- ставлений *-алгебры P2 . Все неприводимые конечномерные *-представления одномерны и двумерны.

1.5. Спектральная теорема. Пусть dimН = n. В этом пункте мы получим разложение на неприводимые *-подпредставления исходного *-представления π *-алгебры P2, а также разложение пространства Н на инвариантные подпространства относительно π.

Теорема 3.1. (спектральная теорема). Существует единственное разложе- ние Н в ортогональную сумму инвариантных относительно Р1 и Р2 подпространств

Н = Н0,0Н0,1Н1,0Н1,1  ((С2Нк)), (1.1.)

где каждому подпространству Нк соответствует одно φк (0, ), φк ≠ φi при к≠i, dimНк = nк (к = 1,…, m). Пусть Рi,j: Н → Нi,j , Рφк: Н → С2Нк – ортопроекторы к = 1,…, m. Тогда существуют единственные разложения операторов

I = P0,0 P0,1 P1,0 P1,1(Рφк), (1.2.)

P1 = P1,0P1,1((Iк )) (1.3)

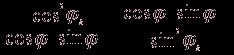
Р2 = P0,1 P1,1  (Iк )) (1.4)

где Iк – единичный оператор на Нк (к = 1,…, m).

Доказательство. Пусть dimНi,j = ni,j. Сразу можем записать разложение

Н = Н0,0 Н0,1 Н1,0 Н1,1  Н΄, где dimН΄ четное число. Используя лемму 1.2. и теорему 2.1. главы I можем написать разложение Н΄ в ортого- нальную сумму инвариантных двумерных подпространств, определяемых параметром φк (0, ):

Н΄ = Нφк, (l = n - )

Собирая вместе все Нφк, у которых одно φк, получим изоморфизм

Нφк…Нφк ≈ С2Нк , где Нφк nк экземпляров, dim(Нφк…Нφк )=2nк dim(С2Нк) = dimС2 dimНк = 2nк . Следовательно, получаем разложение (1.1.)

Н = Н0,0  Н0,1 Н1,0 Н1,1  ((С2Нк))

Пусть πi,j – сужение π на Нi,j ( i, j= 0,1), πк – сужение π на Нφк (к = 1,…, m), то есть πi,j и πк - *-подпредставления.

Учитывая кратности подпредставлений получаем

π = n0,0π0,0n0,1π0,1n1,0π1,0n1,1π1,1(nкπк) (1.5.)

В силу теоремы 2.8. главы I разложения (1.1.) и (1.5.) единственные.

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки