Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

UР1 = Р1U, следовательно U= , a, b C

UР2 (τ) =  =

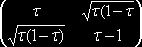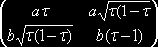
Р2 (ν) U =  = .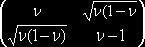

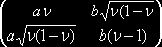Тогда τ = ν, следовательно U = 0 и представления неэквивалентны.

Теорема 1.1. Пусть π: P2 →L(H) - *-представление *-алгебры P2 .

Тогда:

(i) Все одномерные и неэквивалентные представления имеют вид: π0,0(p1) = 0; π0,0(p2) = 0; π1,0(p1) = 1; π1,0(p2) = 0; π0,1(p1) = 0; π0,1(p2) = 1; π1,1(p1) = 1; π1,1(p2) = 1;

(ii) Все двумерные неприводимые и неэквивалентные представления имеют вид: π(p1)  , π(p2)  τ (0, 1).

Доказательство следует из сказанного выше и в пункте (ii) можно положить π(p2) =  φ (0, ).

1.4. n – мерные *-представления *-алгебры P2 . Рассмотрим случай нечетной размерности пространства Н. Если dimН=2n+1, где n>1 натуральное, то выполняется неравенство

max (dimН1, dimН1┴) + max (dimН2, dimН2┴) > 2n+1 (1.4.)

Тогда обязательно найдутся такие i = 0,1 и j= 0,1, что Нi,j ≠ {0}, следовательно, существует нетривиальное инвариантное подпространство относительно *-представления π, но тогда π приводимо.

Пусть теперь dimН=2n, n>1 натуральное. Будем считать, что dimН1 = n, dimН2 = n и Нi,j = {0} для любых i = 0,1 и j= 0,1, то есть Нi,j линейно независимы. Если это не так, то снова будет выполнятся неравенство (1.4.) и *-представление π окажется приводимым. При этих условиях справедлива лемма.

Лемма 1.1. Существует х ≠ 0, хН1 такой, что Р1Р2х = λх, где λС.

Доказательство. Пусть ,  ортонормированный базисы в Н, в которых матрицы операторов Р1 и Р2 имеют вид , где I – единичная матрица порядка n. Пусть базисы (е) и (g) связаны уравнениями

 

к = 1,…, n к = 1,…, n

Так как хН1, то , gk C, к = 1,…, n. Тогда

Р1Р2х = Р1Р2= Р1Р2= Р1=

= Р1= = () =

Таким образом получаем систему линейных однородных уравнений относительно q1,…, qn:

=

j = 1,…, n

Подбирая λC так, чтобы определитель этой системы обратился в нуль, получим ненулевое решение q1,…, qn. Это доказывает лемму.

Лемма 1.2. Пусть элемент х удовлетворяет условиям леммы 15. Тогда L=л.о. {х, Р2х} – инвариантное подпространство в Н относительно Р1 и Р2.

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.



Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки