Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Таким образом А (U + U-1) = (U-1 +U)А (2.2.)

А (U - U-1) = (U - U-1)2А (2.3.)

Пара А и U неприводима (лемма 2.1.), тогда по теореме 2.6. главы I имеем

U + U-1 = cI

(U - U-1)2 = d2I

где c, d С. По теореме преобразования спектров eiφ+ e-iφ = c, eiφ- e-iφ = ±d.

Если d = 0, то (U) состоит из одной точки eiφ, где φ=0 или φ=π, и U = I или U = -I. Так как А, U неприводимая пара, то dimН=1 и А = +I или А = -I. Поскольку существует одномерное инвариантное подпространство y оператора А: л.о. {(A+I)x}, хH.

Если d ≠ 0, то (U) дискретен и состоит из двух точек eiφ= и e-iφ= φ(0, π)

Собственное подпространство оператора U, отвечающее собственному значению eiφ (или e-iφ), Нeiφ = fH одномерно. Действительно, подпространство, натянутое на собственные векторы f и Af для оператора U: Uf = eiφf, U(Аf) = eiφ Аf инвариантно относительно операторов U и А. U и А неприводимы, значит dimНeiφ= dimН-eiφ=1

Таким образом, все неприводимые пары операторов U и А такие, что (U) = {eiφ, e-iφ} φ(0, π) в базисе из собственных векторов оператора U имеют вид:

А = , U = , В =

Теорема 2.2. Неприводимые пары Р1, Р2 ортопроекторов лишь одномер- ны и двумерны.

Доказательство. Сразу следует из леммы 2.2.

2.2. Спектральная теорема. Пусть Н – сепарабельное гильбертово пространство, тогда справедлива следующая теорема.

Теорема 2.3. (спектральная теорема в форме операторов умножения). Паре ортопроекторов Р1 и Р2 в сепарабельном гильбертовом пространстве Н соответствует разложение

Н = Н0,0Н0,1Н1,0 Н1,1 ((С2L2((0, ), dρк))) (2.4.)

где ρ1 > ρ2 >… ρк меры на интервале (0, ), такое, что имеют место равенства

P1 = P1,0 P1,1  ((Iк )) (2.5.)

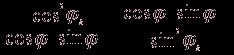
Р2 = P0,1 P1,1 (Iк )) (2.6.)

Iк – единичный оператор в L2((0, ), dρк)

Доказательство. Пространство Н можно представить в виде ортогональной суммы инвариантных подпространств

Н = Н0,0  Н0,1 Н1,0 Н1,1  Н΄, то есть отщепить все одномерные представления от исходного. Н΄ состоит из инвариантных двумерных подпространств.

Всякому положительному функционалу F в *-алгебре P2 отвечает циклическое представление πF *-алгебры P2 в некотором гильбертовом пространстве НF. При этом НF можно реализовать как L2(F), то есть как гильбертово пространство всех функций с интегрируемым квадратом по мере μF на Т.

Пусть каждому вектору ξН поставим в соответствие подпространство Нξ  Н, которое получается замыканием множества векторов вида π(х)ξ, где хА. Ограничения операторов из π(А) на Нξ является циклическим представлением. Обозначим его через πξ, а соответствующую меру на Т через μξ. Введем упорядочение в Н, полагая ξ>η, если μξ > μη (то есть μη абсолютно непрерывна по мере μξ).

Если ηНξ, то НηНξ, тогда πη – циклическое подпредставление πξ. Пусть Е Т и μξ (Е) = 0, тогда μη (Е) = 0, следовательно μξ > μη, а значит ξ>η.

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки