Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

4) Р1 = Р2 = I, то для любого х Н1 = Н2 = Н Ах = Р1х + Р2х = 2х, то есть 2  (А).

Таким образом, если dimH =1, то (А) {0, 1, 2}.

1.4. Спектр в двумерном пространстве. Пусть dimH =2. Сохраним обозначения (1.1.) Главы II.

1) х Н0,0 , тогда Ах = 0 и 0  (А).

2) х Н0,1 или х Н1,0 , тогда Ах = х и 1  (А).

3) х Н1,1, тогда Ах = 2х, то есть 2  (А).

Если существуют i, j= 0,1 такие, что Нi,j ≠ {0}, то существуют k,l = 0,1 такие, что Нi,j  Нk,l = H. В этом случае (А) {0, 1, 2}.

Пусть теперь Нk,l = {0} для любых k,l = 0,1. Допустим, что существует одномерное инвариантное подпространство L относительно Р1 и Р2, тогда АLL. Пусть х L, тогда Рkх = λкх (k = 1, 2 ). Так как Рk ортопроектор, то возможны случаи:

λ1 = 0, λ2 = 0;

λ1 = 0, λ2 = 1;

λ1 = 1, λ2 = 0;

λ1 = 1, λ2 = 1;

Но это означает, что  k,l = 0,1 такие, что Нk,l ≠ {0} вопреки предположению. Тогда пара Р1, Р2 неприводима. Значит мы можем записать матрицы операторов Р1 и Р2 в некотором ортонормированном базисе, согласно теореме 1.1. главы II.

Р1 = , Р2  τ (0, 1)

Найдем спектр линейной комбинации ортопроекторов aР1 + bР2, a и b С. Для этого решим характеристическое уравнение det(aР1 + bР2 – λI) = 0.

 (1.1.)

Тогда 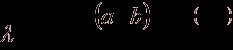,  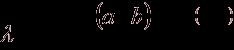(1.2)

Положим a = 1, b =1, ε = , тогда λ1 = 1+ε , λ2 = 1-ε и 0<ε<1 (поскольку 0<τ<1.

Тогда (А) {0, 1, 2}{1+ε , 1-ε}. Причем собственные значения 1+ε и 1-ε входят в спектр А одновременно.

1.5. Спектр в n-мерном пространстве. Пусть dimH =n. Если Н =КL, где К, L инвариантные подпространства относительно оператора А, то для любого х Н существует единственное разложение x = k +l, k K, l L. Пусть λ (А), тогда Ах = λх =λk +λl;, следовательно, если пространство Н разложено в ортогональную сумму инвариантных подпространств, то спектр оператора А можно найти как объединение спектров сужений оператора А на соответствующие инвариантные подпространства.

Используя лемму 1.2. главы II, представим Н в виде ортогональной суммы подпространств Н0 = Н0,0, Н1=Н0,1Н1,0, Н2=Н1,1 и двумерных, инвариантных относительно А, подпространств Нφк φк (0, ), (к = 1,…, s). При этом операторы Р1 и Р2 неприводимы в Нφк (к = 1,…, s), и собственные значения 1+εк, 1-εк входят одновременно в спектр А. Так как А*=А, то соответствующие собственные векторы ортогональны. Тогда имеет место разложение на собственные подпространства

Нφк = Н1+εк Н1-εк , причем dimН1+εк = dimН1-εк = 1 (1.3)

Если φк ≠ φi, то εк ≠ εi (так как εк = =cosφк и φк (0, )). Объединим все Нφк , у которых одинаковые φк , в одно слагаемое, и обозначим его через Нφк. При этом, если dimНφк = 2qk, то есть Нφк состоит из qk экземпляров двумерных подпространств, отвечающих одному φк , то объединяя вместе все соответствующие одномерные собственные подпространства, получим Нφк = Н1+εк Н1-εк , dimН1+εк = dimН1-εк = qk.

Теорема 1.2. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р1 и Р2 тогда и только тогда, когда

(А) {0, 1, 2}({1+ε , 1-ε}), 0<εк<1,

причем dimН1+εк = dimН1-εк к = 1,…, m.

Доказательство. Пусть А = Р1 и Р2, тогда его спектр был найден выше:

(А) {0, 1, 2}({1+ε , 1-ε}), где 0<εк<1для любого к = 1,…, m.

Обратно, пусть нам известен спектр оператора А и известно, что размерности соответствующих собственных подпространств совпадают, то есть

dimН1+εк = dimН1-εк . Существует единственное разложение Н в ортогональную сумму инвариантных подпространств ((1.1.) Глава II):

Н = Н(0) Н(1) Н(2) ((С2Нк)) (1.4.)

(1.4.) можно записать иначе

Н = Н(0) Н(1) Н(2) ((С2(Н1+εк Н1-εк ))) (1.5.)

Зададим ортопроекторы Р1 и Р2 следующим образом

P1 = PН2((Iк )) (1.6.)

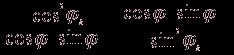
Р2 = PН1 PН2  ( Iк )) (1.7.)

где PНк – ортопроектор в Н на Н(к) (к = 1, 2), Is – единичный оператор в Hs s=1,…, m. Но тогда

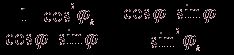
Р1 + Р2 = PН1 PН2  ( Iк )) = А, при этом А = А*

1.6. Линейная комбинация ортопроекторов. Пусть теперь с. Из (1.2.) следует λ1 + λ2 = a + b. Пусть λ2 = ε, тогда λ1 = a + b – ε.

Оценим ε. Заметим, что (a +b)2 – 4ab(1-τ) = (a - b)2 + 4abτ > 0.

Тогда ε = 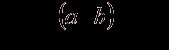 > 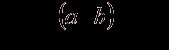= 0, то есть ε = 0.

Допустим, что ε ≥ a , тогда

a ≤

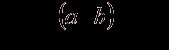
≤ b – a

(b - a)2 +4abτ ≤ (b – a)2

abτ ≤ 0, но abτ > 0 и значит ε < a

Итак,

λ1 = ε

λ2 = a + b – ε. (1.8.)

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки