Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

6. Получим аналитические выражения для частотных характеристик. По определению амплитудная частотная характеристика (АЧХ) - это модуль частотной передаточной функции, т.е.

A(w )=Ѕ W(jw )Ѕ

A(w )=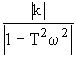=(8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j (w )=argW(jw )

j (w )=argk - arg(1-T2w 2)=0 (9)

Для построения логарифмических частотных характеристик вычислим

L(w )=20lg A(w )

L(w )=20lg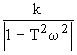 (10)

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.2. ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ

4.2.1. ИНТЕГРИРУЮЩЕЕ ИДЕАЛЬНОЕ ЗВЕНО

 

1. Данное звено описывается следующим уравнением:

a1 =bog(t) (1)

Коэффициенты имеют следующие значения:

a1=1,24

bo=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a1:

=g(t)

=kg(t) (2),

где k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

py(t)=kg(t) (3)

2. Получим передаточную функцию для данного звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

g(t)=G(s)

По определению передаточная функция находится как отношение выходного сигнала к входному. Тогда уравнение (2) будет иметь вид:

sY(s)=kG(s)

W(s)= (4)

3. Найдем выражения для переходной функции и функции веса. По определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1 или по преобразованиями Лапласа

h(t)=H(s)

H(s)=W(s)=

Переходя к оригиналу, получим

h(t)=ktЧ 1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

w(t)==kЧ 1(t) (6)

4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи, постоянные времени и временные характеристики:

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw :

W(s)=

W(jw )= (7)

W(jw )=

U(w )=0

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, реферати українською.



Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки