Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

то уравнение есть уравнение в полных дифференциалах.

Сначала решаем уравнение

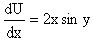или dU=2xsinydx,

считая y постоянной. Интегрирование уравнения дает

U(x,y)=x2siny+h(y).

Затем находим функцию h(y), используя соотношения

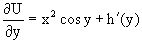, с одной стороны, и 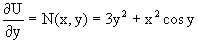, с другой стороны. Соотношения приводят к дифференциальному уравнению

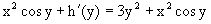или .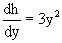

Интегрируя последнее уравнение, получаем h=y3+c.

Тогда общий интеграл исходного дифференциального уравнения записывается в виде

X2siny+y3+c=0.

Далее рассмотрим понятие интегрирующего множителя. Ранее отмечалось, что уравнение в полных дифференциалах возникает, когда поведение системы сохраняет некоторую величину U, т.е. удовлетворяет соотношению

U(x,y)=c.

Дифференциальным аналогом его является уравнение dU(x,y)=0 или

M(x,y)dx+N(x,y)dy=0,

Где .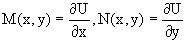

Предположим теперь, что частные производные функции U(x,y) представимы в виде

.

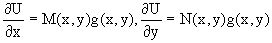Тогда соотношению U(x,y)=e будет соответствовать уравнение в полных дифференциалах вида

M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0.

Если теперь данное уравнение разделить на общий множитель слагаемых g(x,y), то получим уравнение M(x,y)dx+N(x,y)dy=0.

Решение последнего уравнения эквивалентно решению предыдущего, из которого оно получено, однако оно может уже не являться уравнением в полных дифференциалах, также для него возможно будет

.

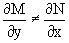В то же время после умножения его на множитель g(x,y), оно становится уравнением в полных дифференциалах.

Определение. Функция g(x,y) называется интегрирующим множителем дифференциального уравнения

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки