Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

вытекает, что для исходного дифференциального уравнения существует интегрирующий множитель g=g(y), с помощью которого уравнение становится уравнением в полных дифференциалах.

Интегрирующий множитель находится из уравнения

.

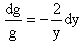Интегрируя его, получаем .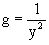

Умножая исходное уравнение на множитель 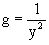, приходим к уравнению

.

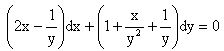Это уравнение является уже уравнением в полных дифференциалах. Решаем его

,

,

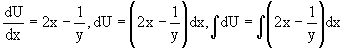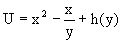затем из

получаем

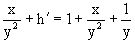или .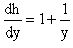

Интегрируя последнее уравнение, имеем .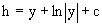

Таким образом, общий интеграл исходного уравнения имеет вид

.

7. Дифференциальные уравнения второго порядка.

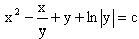Обыкновенное дифференциальное уравнение второго порядка имеет следующий общий вид

F(x,y,y/,y//)=0 или .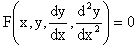

Наше знакомство с дифференциальными уравнениями второго порядка будет ограничено рассмотрением линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

y//+py/+qy=h(x),

где p и q – числа, h(x) – некоторая функция от x.

Если в этом уравнении 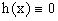, то оно называется однородным линейным дифференциальным уравнением второго порядка.

Рассмотрим решение однородного уравнения

.

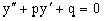Этому явлению может быть поставлено в соответствие квадратное уравнение вида ,

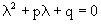Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки