Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

.

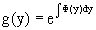Пример 3. Дано уравнение

(y2-3xy-2x2)dx+(xy-x2)dy=0.

Из M(x,y)=y2-3xy-2x2, N(x,y)=xy-x2, 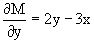, 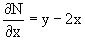следует 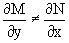, т.е. уравнение не является в полных дифференциалах.

Однако из соотношения

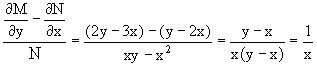
вытекает, что можно найти такой интегрирующий множитель g=g(x), после умножения на который исходное уравнение становится уравнением в полных дифференциалах.

Указанный множитель находим из уравнения

,

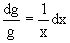интегрируя которое получаем 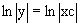, или g=xc. Так как в качестве множителя достаточно взять одну из функций, то положим c=1 и, тогда, g=x.

Умножая исходное уравнение на множитель g=x, получаем

(xy2-3x2y-2x3)dx+(x2y-x3)dy=0,

являющееся уже уравнением в полных дифференциалах. Интегрируя его, находим

,

,

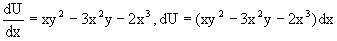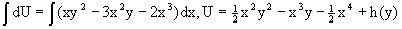затем из U/y=x2y-x3+h/(x) и U/y=N(x,y)=x2y-x3

получаем x2y-x3+h/=x2y-x3, т.е. 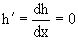и,

следовательно, h=c=const. Таким образом, общее решение имеет вид

.

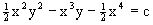Пример 4. Требуется решить уравнение

(2xy2-y)dx+(y2+x+y)dy=0.

Из M(x,y)=2xy2-y, N(x,y)=y2+x+y, 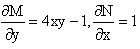следует

.

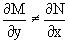Однако из соотношения

,

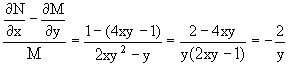Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки